- De acordo com teste da primeira derivada, quais condições garantem que tem um máximo relativo em ? E um mínimo relativo?
- De acordo com o teste da segunda derivada, quais condições garantem que tem um máximo relativo em ? E um mínimo relativo?
Passo 1
- Quando estamos falando do teste da primeira derivada, devemos calcular a derivada e encontrar o ponto onde a derivada zera, isso significa que temos que encontrar a(s) raíz(es) da primeira derivada. Partindo do ponto que possuímos os valores das raízes (ou valor onde não é possível calcular a função), analisamos o(s) sinal da função antes e depois da raiz, se:
- No teste da segunda derivada, devemos conhecer os valores da(s) raíz(es) da primeira derivada. Então, calculamos a segunda derivada, aplicamos o(s) valor(es) da(s) raíz(es) da primeira derivada na segunda derivada e analisamos o sinal. Quando temos:
Máximo Relativo: Para valores de a esquerda de tendo e valores de a direita de tendo
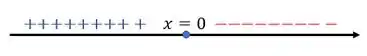
Máximo Relativo: Para valores de a esquerda de tendo e valores de a direita de tendo
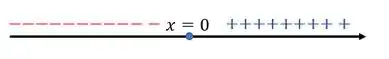
Passo 2
Máximo Relativo: e .
Mínimo Relativo: e
Resposta
Ei, a resposta está no passo a passo :)