Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.4 - Ex. 7
7. Para o limite:
Ilustre a definição 2 encontrando os valores de que correspondam a e
Passo 1
Opa, vamos fazer essa questão! Temos o seguinte limite:
E o enunciado pede pra a gente aplicar a definição 2 de limite no limite acima, achando os valores de para a e . Vamos então relembrar a definição de limite:
Se para todo número houver um número tal que:
Se então
Vamos reescrever essas condições sem os módulos e substituir nossas condições pra ficar mais fácil de visualizar:
Bora colocar a mão na massa?
Passo 2
Do enunciado, temos o seguinte:
A primeira coisa que vamos fazer é plotar o gráfico :
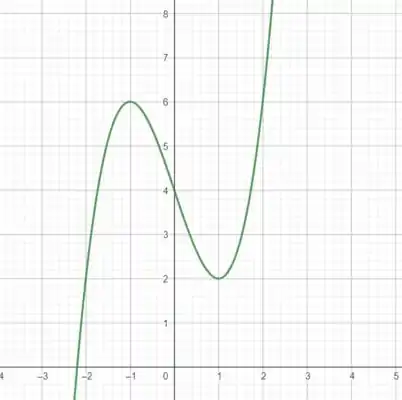
É importante podermos visualizar as proximidades de , então vamos dar um zoom:
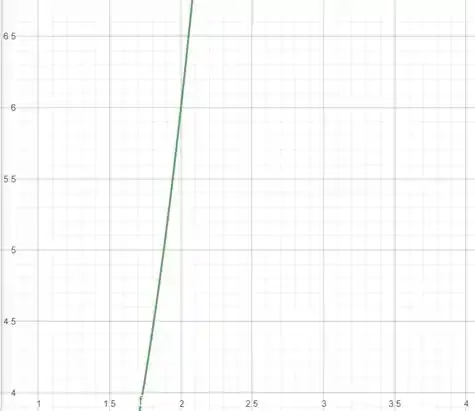
Usando a definição de limite, para :
Vamos usar o gráfico pra achar e :
Dessa forma temos:
É claro que pra enxergar esse valor você vai ter que dar um suuuuper zoom!
Lembrando que, pelo teorema de limite:
Então:
Como nossos valores de tem que ficar naquela faixa, vamos pegar o menor . Assim:
Passo 3
Agora, para :
Pelo gráfico temos o seguinte:
Calculando :
Como nossos valores de tem que ficar naquela faixa, vamos pegar o menor . Assim: