Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.1 - Ex. 15

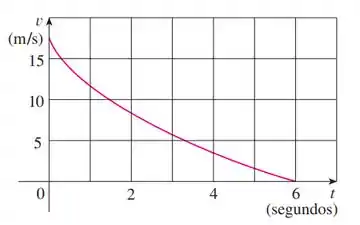
O gráfico da velocidade de um carro freando é mostrado. Use-o para estimar a distância percorrida pelo carro enquanto os freios estão sendo aplicados.

Passo 1

Olá, meu querido amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui temos um gráfico de velocidade tempo e a partir dele deveremos encontrar o espaço total percorrido.

Para uma função decrescente, usando pontos extremos esquerdos, temos uma superestimativa, e usando pontos extremos direitos, temos uma subestimativa.

A distância percorrida é a área sob a curva da velocidade pelo tempo. Podemos fazer uma estimativa dividindo o tempo total em intervalos, e estimando a distância percorrida em cada intervalo.

Passo 2

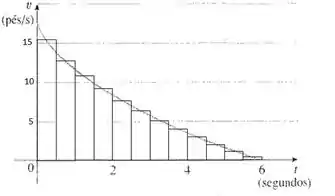
Vamos dividir em intervalos de 0,5 segundo. Temos então 12 intervalos. Consideraremos que a velocidade em cada intervalo é a velocidade no meio dele. Vamos fazer isso por que se escolhermos a velocidade inicial estaremos superestimando muito o valor verdadeiro da distancia, e se escolhermos a final estaremos subestimando muito.

Então o desenho dos retângulos aproximastes da área fica assim:

Passo 3

Então vamos tentar olhar a velocidade no meio de cada intervalo de 0,5s. A distância em cada intervalo será d=0,5*v.

Nós usaremos para termos nossa estimativa. , como é possível ver no gráfico.

Para conseguirmos calcular, precisaremos entender cada um dos subintervalos divididos no gráfico, ou seja, até chegarmos no tempo de 6s, passamos por 12 intervalos de 0,5s.

Assim, vamos seguir pelo gráfico o valor da velocidade em cada um destes intervalos:

De 0s a 0,5s: 17m/s

De 0,5 a 1s: 12,5 m/s

De 1 a 1,5s: 11 m/s

De 1,5 a 2s: 9 m/s

De 2 a 2,5s: 7,5 m/s

De 2,5 a 3s: 6 m/s

De 3 a 3,5s: 5 m/s

De 3,5 a 4s: 4 m/s

De 4 a 4,5s: 3 m/s

De 4,5 a 5s: 2 m/s

De 5 a 5,5s: 1 m/s