Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.1 - Ex. 10
- Se , use os comandos discutidos no Exercício 9 para encontrar as somas esquerda e direita para , e .
- Ilustre fazendo o gráfico dos retângulos da parte (a).
- Mostre que a área exata sob está entre 0,87 e 0,91.
Passo 1
Oieee, tudo bem? Vamos de mais uma resolução hoje.
Dada a função:
Dentro do intervalo:
Vamos utilizar os comandos do exercício para resolver essa atividade. Aqui eu preciso que você tenha resolvido o exercício antes de continuar, mas irei te mostrar os códigos para você relembrar.
Quando temos uma soma a esquerda, o nosso intervalo se torna:
E para uma soma a direita:
O Código que iremos utilizar aqui, é o seguinte:
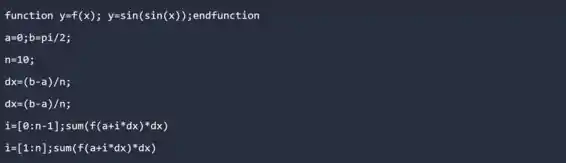
Definimos a nossa função, nosso intervalo e o nosso . Depois também definimos os nossos , e aí temos os nossos intervalos de . Lembre-se que o que é feito nessas somas é calcular a área infinitesimal, dividindo a função em intervalos, e calculando cada pequena porção de área.
Veja abaixo o retângulo:
Ele tem um lado esquerdo, e um lado direito, além da sua base. Quando utilizamos o lado esquerdo do retângulo como o nosso valor da ‘altura’ estamos utilizando o método de pontos finais a esquerda, e quando utilizamos o lado direitos, estamos utilizando o método de pontos finais a direita.
Passo 2
(a) Utilizando um programa, calculamos as somas esquerda e direita dos retângulos aproximantes para os três valores de e obtemos:
Direita:
Esquerda:
Direita:
Esquerda:
Direita:
Esquerda:
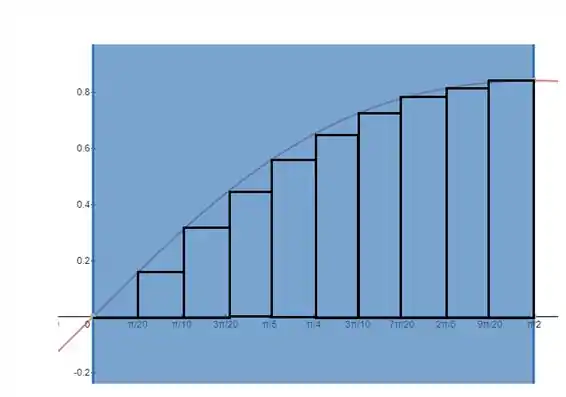
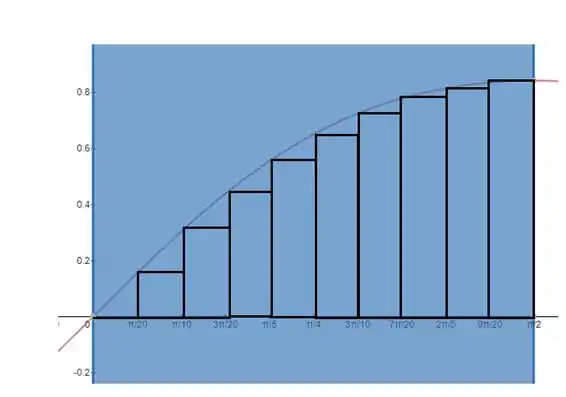
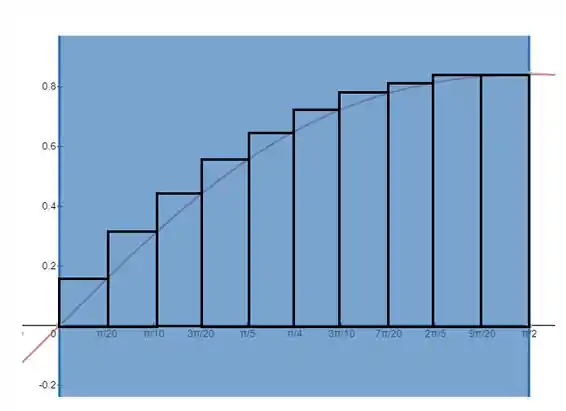
(b) Vamos mostrar os retângulos para pela esquerda e pela direita.
Os retângulos para e são construídos da mesma forma, mas com intervalos menores e mais retângulos. Para , cada intervalo tem um tamanho:
Para a soma direita, pegamos como altura de cada retângulo o valor da função no final de cada pequeno intervalo de tamanho . Por exemplo, o primeiro retângulo tem base indo de ate e sua altura é .
Com auxílio de uma ferramenta gráfica construímos o gráfico da função. Nossos retângulos então ficam assim:
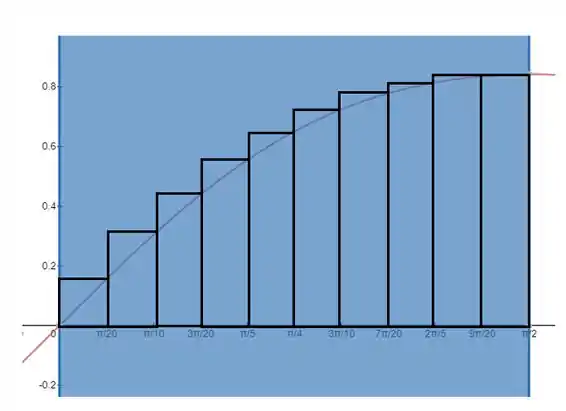
Para a soma direita, pegamos como altura dos retângulos os valores da função no início de cada intervalo:
Passo 3
- Como podemos ver no item (b) pelas imagens, a aproximação direita calcula um valor que é na verdade maior que a área exata sob a curva, enquanto a aproximação esquerda calcula um valor que é menor.
No item (a), para calculamos para a aproximação direita um valor de aproximadamente 0,906 e para a aproximação esquerda aproximadamente 0,88.
Então, o valor exato da área é menor que 0,906 e maior que 0,88. Consequentemente, está entre 0,91 e 0,87.
Resposta
-
Direita:
Esquerda:
Direita:
Esquerda:
Direita:
Esquerda:
- Ver o desenvolvimento.
