Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.1 - Ex. 14
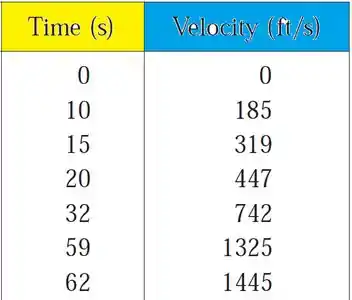
Quando estimamos as distâncias a partir dos dados das velocidades, algumas vezes é necessário usar tempos ... que não estão igualmente espaçados. Podemos ainda estimar as distâncias usando o período de tempo . Por exemplo, em 7 de maio de 1992, o ônibus espacial Endeavor foi lançado na missão STS-49 cujo propósito era instalar o satélite de comunicação Intelsat. A tabela, fornecida pela NASA, mostra os dados de velocidade do ônibus entre o lançamento e a entrada em funcionamento dos foguetes auxiliares. Utilize esses dados para estimar a altura do ônibus espacial, acima da superfície da Terra, 62 segundos após seu lançamento.
Passo 1
Olá, meu querido amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui temos os dados das velocidades e do tempo do lançamento de um ônibus espacial, e a partir disso iremos encontrar a altura do ônibus espacial.
Vale relembrar que a relação entre velocidade, tempo e espaço é dada por:
Então o que iremos fazer é, a partir da velocidade num ponto e o tempo percorrido até chegar aquele ponto, iremos descobrir o deslocamento, e após somarmos todos os deslocamentos iremos finalmente descobrir a altura aproximada do ônibus.
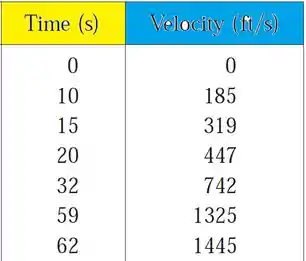
Os dados são oriundos da tabela, irei te apresentar ela no próximo passo.
Passo 2
Podemos fazer uma estimativa para a altura considerando que a velocidade em cada intervalo de tempo é constante. Vamos fazer uma estimativa superior, estimando que a velocidade em cada intervalo é a velocidade no final dele. Então, a distância percorrida em cada intervalo é:
Sendo a distância percorrida do tempo até o tempo , com indo de 1 até 6, pois . A distância total é então:
