Alguns sistemas algébricos computacionais têm comandos que traçam retângulos aproximantes e calculam as somas de suas áreas, no mínimo se é um extremo esquerdo ou direito.
- Se , , ache as somas esquerda e direita para , , e .
- Ilustre fazendo o gráfico dos retângulos da parte (a).
- Mostre que a área exata sob está entre 4,6 e 4,7.
Passo 1
(a) Utilizando um programa, calculamos as somas esquerda e direita dos retângulos aproximantes para os três valores de e obtemos:
Direita:
Esquerda:
Direita:
Esquerda:
Direita:
Esquerda:
Passo 2
(b) Vamos mostrar os retângulos para pela esquerda e pela direita. Os retângulos para e são construídos da mesma forma, mas com intervalos menores e mais retângulos. Para , cada intervalo tem um tamanho:
Para a soma direita, pegamos como altura de cada retângulo o valor da função no final de cada pequeno intervalo de tamanho 0,3. Por exemplo, o primeiro retângulo tem base indo de ate e sua altura é . Nossos retângulos então ficam assim:
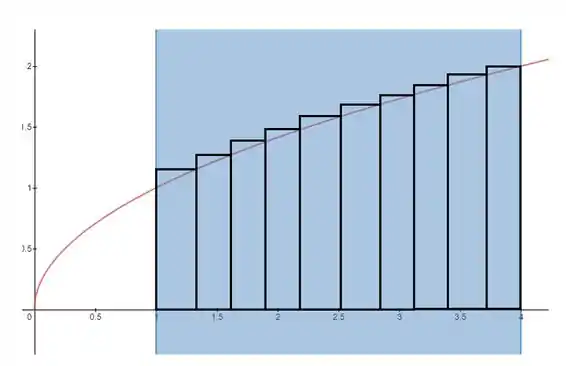
Para a soma direita, pegamos como altura dos retângulos os valores da função no inicio de cada intervalo:
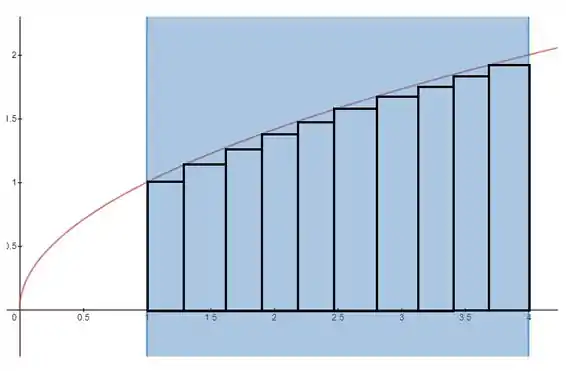
Passo 3
(c) Como podemos ver no item (b) pelas imagens, a aproximação direita calcula um valor que é na verdade maior que a área exata sob a curva, enquando a aproximação esquerda calcula um valor que é menor. No item (a), para calculamos para a aproximação direita um valor de aproximadamente 4,7 e para a aproximação esquerda aproximadamente 4,7. Então, o valor exato é menor que 4,7 e maior que 4,6.
Resposta
Ei, a resposta está no passo a passo :)