Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.1 - Ex. 3 f
O gráfico de uma função é dado:
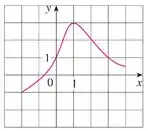
f) Em qual intervalo é crescente?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu o gráfico de uma função e pediu pra gente determinar o intervalo onde ela é crescente. O que isso quer dizer?
O intervalo que a função é crescente é quando o valor de aumenta toda vez que aumenta um pouquinho.
Então, vamos analisar a nossa curva e os valores que ela assume em em para determinarmos o intervalo de crescimento da função.
Vamos lá!
Passo 2
Vamos começar colocando na tabela abaixo, alguns valores para e conforme a função:
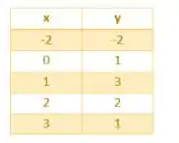
Quando sai de e vai para o valor de sai de e vai para . Isso quer dizer que aumentou conforme íamos aumentando o
Mas quando sai de e vai o valor de sai de e vai para . Isso quer dizer que diminuiu conforme íamos aumentando o
Então, conforme a definição, podemos concluir que a função é crescente quando .
Assim, vendo no gráfico, será essa parte pontilhada que está ascendente:
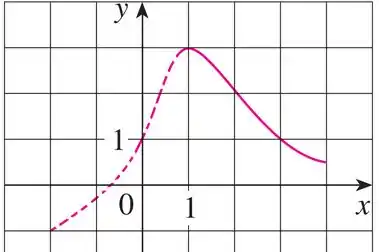
Ufaaa, terminamos!
Valeu, galera! Até a próxima! 😉