Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.3 - Ex. 56
Um avião voa a uma velocidade de , a uma altitude de e passa diretamente sobre uma estação de radar no instante
- Expresse a distânciahorizontal de voo (em quilômetros) como uma função de .
- Expresse a distância entre o avião e a estação de radar como uma função de .
- Use composição para expressar como uma função de
Passo 1
Bom, foi dado que o avião está a da superfície, e essa distância não vai mudar ao longo do percurso. Além disso, a velocidade é de . Temos que descobrir na letra (a) como é a função da distância que o avião percorreu, de acordo com o tempo .
Para isso, na letra (a), temos que pegar o instante (em horas) que queremos e multiplicar pela distância que ele percorre em :
Primeiro passo concluído.
Passo 2
Agora, para a letra (b), a gente vai ter que analisar melhor a situação.
Podemos ver que se forma um triângulo retângulo, como na figura:
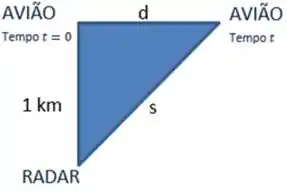
Assim, a distância entre o avião e o radar é, pelo teorema de Pitágoras:
Como depende de , podemos colocar a notação
Beleza!
Passo 3
Agora, para a letra (c), queremos uma função que expresse a distância entre o avião e a estação de radar, de acordo com o tempo que se passou. Já temos a função dependendo da distância , e já temos a função dependendo do tempo. Basta fazermos a composição .
Vamos substitui todo da função de (do passo 2) pela função inteira de (do passo 1):
Pronto!