Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.1 - Ex. 3 c
O gráfico de uma função é dado:
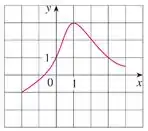
b) Para quais valores de é ?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu o gráfico de uma função e pediu pra gente encontrar o valor de para , ou seja, o valor de no ponto .
Pra isso, vamos encontrar o ponto e traçar uma reta horizontal paralela ao eixo até encontrar a curva. Depois marcamos os pontos de interseção entre a reta e a curva para encontrar os valores de .
Vamos lá!
Passo 2
Vamos começar traçando a reta paralela ao eixo , partindo de , até encostar na curva da função
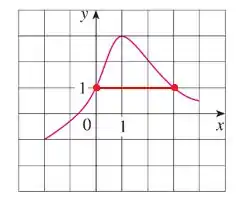
Agora vamos verificar os valores de correspondentes a :
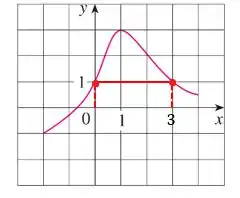
Repare que existem dois valores de para , que são e . Assim, temos:
E encontramos a nossa resposta.
Valeu, galera! Até a próxima! 😉
Resposta
Exercícios de Livros Relacionados
Calcule: b )g 0 ,g ( 2 ) e g 2 sendo g x = x x 2 - 1
Simplifique f x - f ( p ) x - p( x ≠ p ) sendo dados: j ) f x = 1 x ,ep = 1
Simplifique f x - f ( p ) x - p( x ≠ p ) sendo dados: e ) f x = 2 x + 1 ,ep = - 1
Calcule: d ) f a + b - f a - b a b , sendo f x = 3 x + 1 e a b ≠ 0
Simplifique f x - f ( p ) x - p( x ≠ p ) sendo dados: n ) f x = 1 x 2 ,ep = 3