Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 20b
Dados dois pontos A(-3,4) e B(2,5), ache as coordenadas de um ponto P sobre a reta que passa por A e B, tal que P seja duas vezes mais distante de B do que de A.
Passo 1
Queremos encontrar de forma que a distância entre e B seja o dobro da distância entre P e A, ou seja, A é o ponto médio do segmento PB. Logo, da definição de ponto médio, temos
Montando os sistemas, temos
E também
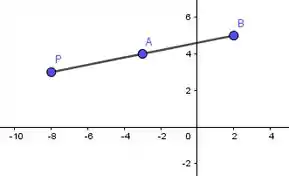
Resposta
Portando, o ponto procurado é P(-8, 3).
Exercícios de Livros Relacionados
Encontre as equações da reta que passa pelo ponto Q = (1, 2, 1) e é perpendicular ao plano x - y + 2 z - 1 = 0
Determine as equações paramétricas da reta interseção dos planos: x - y = 0ex + z = 0
Determine as equações paramétricas da reta interseção dos planos: x + 2 y - 3 z - 4 = 0 ex - 4 y + 2 z + 1 = 0
Ache equações da reta que passa pelo ponto P = (1, 0, 1) e é paralela aos planos 2 x - y + 3 z - 1 = 0ex - y + z = 0 .