Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.7 - Ex. 3

Estime ∫ 0 1 cos ⁡ x 2 d x usando (a) a Regra do Trapézio e (b) a Regra do Ponto Médio, cada qual com n = 4 . A partir de um gráfico do integrando, decida se suas estimativas são subestimadas ou superestimadas. O que você pode concluir sobre o valor verdadeiro da integral?

Passo 1

  1. Para achar a aproximação pela Regra do Trapézio temos a fórmula abaixo, onde temos o intervalo 0 ≤ x ≤ 1 , e vamos usar n = 4 , temos que ∆ x :

    2. ∆ x = b - a n = 1 - 0 4 = 1 4

    T 4 = 1 2 ∆ x f x 0 + 2 f x 1 + f x 2 + 2 f x 3 + f x 4 = 1 2 ∙ 1 4 f 0 + 2 f 1 4 + f 2 4 + 2 f 3 4 + f 1 = 1 8 f 0 + 2 f 1 4 + f 2 4 + 2 f 3 4 + f 1

    Substituindo os valores de f em f x = cos ⁡ x 2 vamos ter:

    T 4 = 1 8 f 0 + 2 f 1 4 + f 2 4 + 2 f 3 4 + f 1 ≈ 0,895759

    Passo 2

  2. Para a regra do Ponto Médio temos, onde os x dos pontos são os pontos médios de cada intervalo:

M 4 = ∑ i = 1 n f x i - ∆ x = f 1 8 + f 3 8 + f 5 8 + f 7 8 1 4   ≈ 0,908907

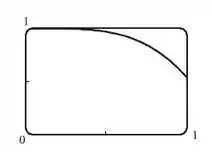
A partir do gráfico vemos que f é côncava para baixo em 0,1 , assim T 4 é subestimada e M 4 é superestimada. Podemos concluir que o valor verdadeiro da integral é:

0,895759 < ∫ 0 1 cos ⁡ x 2 d x < 0,908907

Resposta

  1. T 4 ≈ 0,895759
  2. M 4   ≈ 0,908907
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a soma de Riemann para a função no intervalo, usando a partição Δ das e os valores de ξ i dados. Faça um esboço do gráfico da função no intervalo dado e mostre os retângulos cujas medidas de área
Ache a soma de Riemann para a função no intervalo, usando a partição Δ das e os valores de ξ i dados. Faça um esboço do gráfico da função no intervalo dado e mostre os retângulos cujas medidas de área
Ache a soma de Riemann para a função no intervalo, usando a partição Δ das e os valores de ξ i dados. Faça um esboço do gráfico da função no intervalo dado e mostre os retângulos cujas medidas de área
Ache a soma de Riemann para a função no intervalo, usando a partição Δ das e os valores de ξ i dados. Faça um esboço do gráfico da função no intervalo dado e mostre os retângulos cujas medidas de área
Nos exercícios de 25 a 28, ache o valor exato da integral definida usando a definição; não utilize o teorema fundamental do cálculo.