Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.4 - Ex. 18
Demonstre cada afirmação usando a definição , de limite e ilustre com um diagrama como o da Figura 9.
Passo 1
E aí, tudo bem?! Aqui temos o limite:
Aqui a gente precisa demonstrar o limite acima usando a definição e .
Beleza, mas que definição é essa?! Imagina que tenhamos o seguinte limite:
Então para todo número , nós precisamos achar , tal que se:
Então:
Podemos escrever essas expressões sem os módulos pra ficar mais fácil de visualizar!
Pra resolver esse problema vamos substituir os nossos dados nessas expressões aí de cima! Com elas em mente, vamos pegar essa segunda expressão e manipular ela até chegar na primeira. Assim a gente consegue relacionar e !
Depois também temos que fazer um diagrama como da figura do livro:
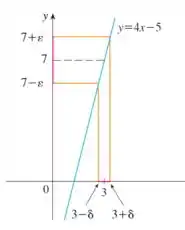
Ou seja, vamos traçar a reta , pegar um intervalo em torno de verificar que existe um intervalo “positivo” em torno de .
Passo 2
Lembra que temos:
Então:
Vamos então vamos começar dando uma arrumadinha na segunda expressão:
Agora vamos dividir todo mundo por :
Multiplicando todo mundo por :
Que é o mesmo que:
Lembra que:
Então:
Passo 3
Podemos então escrever:
Temos que:
Como temos:
Então pra temos um nas condições acima!
Passo 4
Agora vamos desenhar o diagrama! A nossa função é:
Desenhando:
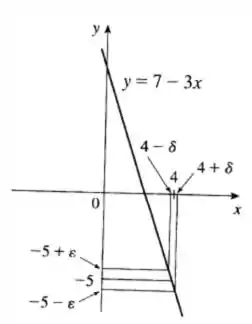
Repara que temos um intervalo em torno de e um intervalo em torno de !
Resposta
Demonstração.