Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 38
Dentre as infinitas retas tangentes à curva que passam pela origem, existe uma que tem a maior inclinação. Use o método de Newton para encontrar a inclinação daquela reta com precisão de seis casas decimais.
Passo 1
Fala meus queridões e queridonas e queridones!
Nessa questão temos a seguinte curva
E queremos encontrar uma reta tangente a curva que passa pela origem que possua a maior inclinação possível.
Temos que então sua derivada é .
Em , a inclinação da reta tangente é
A equação de uma reta é dada por:
A equação de uma reta que passe pela origem e que passe pelo ponto é
Sendo , logo:
E é a inclinação da reta. Como ela é tangente a função , teremos que essa inclinação é igual a sua derivada em , logo:
O método de Newton é usado para encontrar a raiz de uma função
Ele é um método iterativo, onde a partir de um chute inicial você encontrar novos valores para a raiz a partir da seguinte fórmula:
Passo 2
Para aplicar o método de Newton, vamos usar sua fórmula, com
, então a fórmula fica:
Vamos agora precisar de , vamos calcular então!!
Vamos calcular :
Passo 3
Pronto, agora que temos é só jogar na fórmula de Newton:
Vamos agora analisar qual valor usar para , pelo gráfico abaixo, vamos usar .
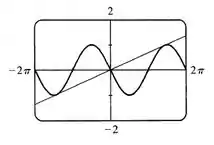
Você pode pensar, por que não procurar por valores maiores que ? Percebe que queremos a máxima inclinação... Valores mais distantes da origem, terão uma inclinação menor. O de maior inclinação é aquele que está próximo do primeiro pico com e positivos.
Usando , teremos:
Como queremos uma precisão de seis casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:
Mais uma vez, agora com :
Agora com :
Vamos agora calcular para achar o valor da maior inclinação da reta:
A inclinação da reta com a máxima inclinação é .
Resposta
A inclinação da reta com a máxima inclinação é .