Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 39
Use o método de Newton para encontrar as coordenadas, com precisão de seis casas decimais, do ponto na parábola que esteja mais próximo da origem.
Passo 1
Fala aí, tudo bem com você?
Bom, essa questão pede pra gente usar o método de Newton para encontrar, com precisão de seis casas decimais, os pontos na parábola
que estejam mais próximos da origem.
E para isso, vamos relembrar o que é esse tal método de Newton.
Nele vamos considerar uma reta tangente à curva da função no ponto .
Depois devemos procurar a interseção de como o eixo , que será chamada de e verificar o quão próximo está da interseção da curva com o eixo .
Para encontrar , podemos fazer:
Depois, repetimos o processo, usando como uma segunda aproximação, fazendo:
E podemos repetir o processo quantas vezes for necessário. De modo geral, fazendo
E se ficar cada vez mais próxima da raiz de nossa curva à medida que cresce, fizemos que a sequência converge para .
Assim:
Perfeito. Então vamos usar essa ideia para encontrar o que o exercício pediu.
Mas como queremos o ponto mais próximo, temos que lembrar que precisamos minimizar a distância de até um ponto arbitrário na curva , vamos lembrar a fórmula da distância:
Substituindo a expressão da curva na fórmula da distância ficamos com:
Temos que quando , vai ser minimizado e de forma equivalente também será minimizada.
Então usamos o método de Newton com e .
Passo 2
Vamos começar fazendo:
Temos que:
E derivando com a regra da cadeia e a regra do expoente, ficamos com:
Maravilha.
Passo 3
Para aplicar o método de Newton, vamos usar sua fórmula:
Vamos substituir na fórmula de Newton:
Vamos agora analisar qual valor usar para , pelo gráfico abaixo, vamos usar , pronto, agora é só substituir, vai ser cansativo, mas vamos lá:
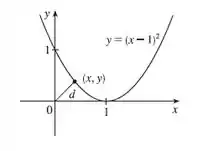
Como queremos uma precisão de seis casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:
Mais uma vez, agora com :
Agora com :
Passo 4
Vamos agora calcular para achar o valor da menor distância:
E para calcular o ponto vamos usar e calcular subatituindo na equação da curva:
Resposta
O ponto é .