Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 69
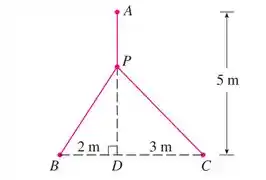
Um pontoprecisa ser localizado em algum ponto sobre a reta de forma que o comprimento totalde fios ligando aos pontos , e seja minimizado (veja a figura). Expresse como uma função de e use os gráficos de e para estimar o valor mínimo de .
Passo 1
Fala aí, tudo certo com você?
Esse exercício dá para gente a imagem
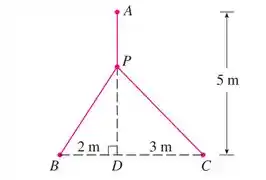
E fala de um pontolocalizado sobre a reta de forma que o comprimento totalde fios ligando aos pontos , e seja minimizado.
Ele quer que a gente expresse como uma função de e use os gráficos de e para estimar o valor mínimo de .
Para fazer tudo isso teremos que encontrar uma expressão que uma todos os pontos dados e assim encontrar o comprimento total do fio. Depois isso faremos sua derivada igualada a zero para minimizar seu valor.
Chamaremos o comprimento de para facilitar nossa resolução.
Passo 2
Já chamamos de , agora, para encontrarmos , precisamos de e , e os encontraremos por meio da aplicação do Teorema de Pitágoras nos triângulos e .
Veja:
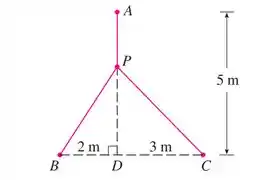
Nos dois triângulos precisamos da altura para calcularmos, então:
Agora já podemos substituir tudo em !
E essa é a expressão que nos dá o comprimento total do fio.
Passo 3
Agora vamos nos preocupar em minimizar seu valor, fazendo sua derivada.
Para isso usaremos a regra da cadeia nos termos que estão dentro da raiz quadrada. Assim a derivada será dada por:
E para minimizar seu valor, faremos:
E como essa é uma expressão bem difícil de ser resolvida, faremos de forma computacional.
Passo 4
Esboçando os gráficos de e , teremos:
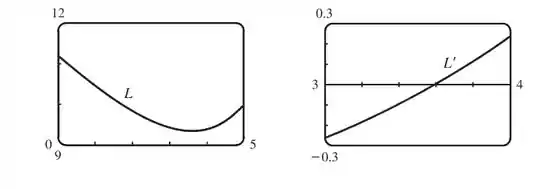
Analisando os dois gráficos vemos que ocorre entre e . Se calcularmos, acontece exatamente em , então o valor mínimo de é:
Resposta
Valor mínimo de : .