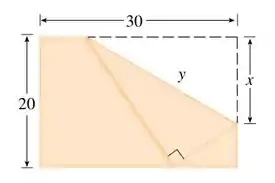
O canto superior direito de um pedaço de papel com de largura por de comprimento é dobrado sobre o lado direito, como na figura. Como você dobraria de forma a minimizar o comprimento da dobra? Em outras palavras, como você escolheria para minimizar ?
Passo 1
Fala aí, pessoal.
Essa questão dá pra gente um pedaço de papel retangular de dimensões por , e diz que ele será dobrado da maneira representada na imagem:
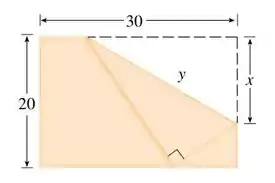
E precisaremos dizer o tamanho de indicado na figura para que a medida de seja a menor possível.
Para isso, vamos escrever a medida em função de e depois fazermos sua minimização através da sua derivada igualada a zero.
Então vamos nessa.
Passo 2
Para escrever em função de , a gente vai precisar de mais detalhes do que esses que a figura nos dá, então esboçaremos um novo desenho. Veja:
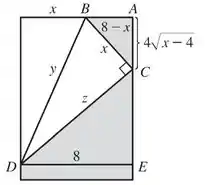
O pedaço foi encontrado aplicando o teorema de Pitágoras, fazendo:
E desenvolvendo:
Ou melhor:
E isolando , teremos:
Maravilha.
Passo 3
O exercício quer que minimizemos em função de , então primeiramente encontraremos uma fórmula que inclui as duas variáveis, sendo:
Essa fórmula ainda não está muito bonita, porque depende de , mas também de outra variável, , então precisamos encontrar uma fórmula no nosso desenho que isola em função de .
Veja:
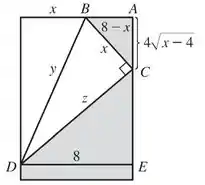
Os triângulos e são semelhantes, pois ambos têm um ângulo de , e os dois tem os outros dois ângulos sendo complementares ao nosso triângulo chave , então:
E simplificando:
Passo 4
Lembrando que
Chamaremos para facilitar um pouco as contas.
E substituindo , teremos:
E desenvolvendo, ficamos com
Assim, tirando o mmc, teremos:
Passo 5
Agora vamos procurar mínimo, mas lembra que fizemos .
Então podemos procurar mínimo que tem uma expressão mais simples e tem mínimo igual ao mínimo de .
Assim, minimizando através de sua derivação, teremos:
E sua derivada será calculada usando a regra do quociente. Fazendo:
Assim:
E desenvolvendo, ficamos com:
Agora igualando a zero, ficamos com:
E como o denominador não pode zerar, teremos
Ou
Veja que não pode ser zero pois se trata de uma medida, então, o que minimiza é .