Encontre a área máxima do retângulo que pode ser circunscrito em torno de um dado retângulo com comprimento e largura . [Sugestão: Expresse a área como uma função do ângulo .]
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão pede pra gente encontrar a área máxima do retângulo que pode ser circunscrito em torno de um dado retângulo com comprimento e largura .
Além disso, ela nos dá a sugestão de expressar a área como uma função do ângulo .
Assim, esboçando os dados do enunciado num desenho temos:
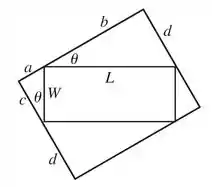
Perceba que agora podemos determinar a área desse retângulo circunscrito em função de .
E a área que queremos maximizar será dada por:
E para achar seu valor máximo, faremos sua derivada igualada a zero. Assim, estamos procurando:
Vem comigo que te mostro tudo isso no passo a passo.
Passo 2
Como nossa fórmula ainda depende de muitas variáveis, vamos usar os recursos dados pela figura para isolá-las.
No pequeno triângulo com lados e e hipotenusa temos:
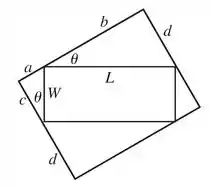
No triângulo com lados e hipotenusa temos:
Substituindo em
E fazendo as multiplicações distributivas, ficamos com:
Ou melhor:
E como , podemos escrever:
Com:
Perfeito.
Passo 3
Essa expressão mostra, sem cálculos, que o máximo valor de ocorre quando:
Conseguimos ver isso porque o seno de , que é o valor máximo que a função pode atingir.
Então a máxima área é:
Resposta
Área máxima: