Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 32
Descreva a mudança no gráfico de à medida que varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos de máximo e mínimo e os pontos de inflexão movem-se quando varia. Você deve também identificar qualquer valor intermediário de no qual o aspecto básico da curva mude.
Passo 1
Nós vemos que para é apenas definida em , e , desde que é .
Assim, para , há assíntotas verticais em , e conforme diminui (, as assíntotas se distanciam mais.
Para , , então há uma assíntota vertical em .
Se , não há assíntota.
Passo 2
Para encontrarmos os pontos extremos e de inflexão, fazendo as derivadas:
Assim, vemos que há um ponto extremo em .
Fazendo a segunda derivada, temos
Assim, se , é sempre negativa, então é côncava para baixo nos dois intervalos onde é definida. Se , então muda o sinal quando . Se para há pontos de inflexão em , e aumenta, os pontos de inflexão se afastam.
Passo 3
Esboço do gráfico:
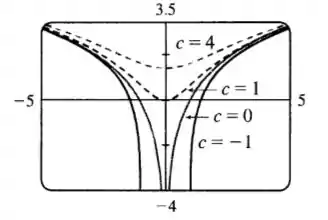
Resposta
Ei, a resposta está no passo a passo :)