Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 39

Investigue a família de funções polinomiais dada pela equação . Para quais valores de a curva tem pontos de mínimo?

Mostre que os pontos de máximo e de mínimo de cada curva da família estão sobre a parábola . Ilustre fazendo o gráfico dessa parábola e de vários membros da família.

Passo 1

Oi, pessoal! Belezinha? Vamos resolver essa questão juntos!

Temos uma família de funções que dependem de um parâmetro da seguinte forma:

Observe que para cada valor de a função será diferente. Sendo assim, a questão pede para:

Encontrarmos para quais valores de a curva tem pontos de mínimo.

Para fazer isso, vamos encontrar os pontos críticos da função e analisar, usando o Teste da Segunda Derivada, se eles são pontos de mínimo ou não.

Mostrar que os pontos de máximo e de mínimo de cada curva da família estão sobre a parábola .

Para isso, para cada ponto de máximo e de mínimo (que foram obtidos no item anterior) vamos analisar se os pontos , estão no gráfico da parábola.

Vamos ilustrar algumas curvas da família e o gráfico da parábola, utilizando uma ferramenta gráfica.

Obs.: Você também pode tentar esboçar alguns desses gráficos por conta própria, lembrando sempre do Roteiro para Esboçar uma Curva dado no Capítulo , Seção , do livro 😉.

Algumas informações que vão nos ajudar a resolver a questão são:

Todo ponto de máximo ou mínimo da função é um ponto crítico da função, ou seja, é um zero da derivada .

Dado um ponto crítico , podemos decidir se este ponto crítico é um ponto de máximo ou mínimo olhando para o sinal da segunda derivada da seguinte forma:
- Se , o ponto é um ponto de mínimo.
- Se , o ponto é um ponto de máximo.

Passo 2

Investigue a família de funções polinomiais dada pela equação . Para quais valores de a curva tem pontos de mínimo?

Vamos começar encontrando a primeira e a segunda derivada de

Como as funções da família são polinômios, então vamos usar a Regra da Potência em cada um dos seus termos. Relembrando da Regra da Potência:

Dessa forma, a primeira derivada de é dada por

e derivando novamente, obtemos a segunda derivada de dada por

Agora que temos ambas as derivadas, vamos encontrar os seus pontos críticos no próximo passo.

Passo 3

Para encontrar os pontos críticos de

precisamos encontrar os zeros da derivada , ou seja, precisamos encontrar as raízes da equação

Reescrevendo a expressão da função , vamos ter que

Observe que para termos que

tem que valer

Da primeira igualdade temos que é uma raiz, né? Logo, é um ponto crítico.

Já pela segunda igualdade, vamos ter que

ou seja,

Dessa forma,

são duas outras raízes, logo, pontos críticos.

É importante observar que esses pontos só existem se , beleza?

Passo 4

Bem, agora podemos avaliar a segunda derivada

nos pontos críticos encontrados.

Para , temos

Logo, é um ponto de máximo local para todas as funções da família.

Para e , temos que

Logo, para as funções da família que possuem , temos que são pontos de mínimo locais.

Dessa forma, respondendo ao item (a), a curva vai ter pontos de mínimo só quando

Passo 5

Mostre que os pontos de máximo e de mínimo de cada curva da família estão sobre a parábola . Ilustre fazendo o gráfico dessa parábola e de vários membros da família.

Vamos encontrar o valor da função no ponto de mínimo e nos pontos de máximo , para

Observe que:

Para , temos que

Note que , portanto o ponto pertence a parábola

Para temos que

Fazendo as contas, temos que

ou seja,

Portanto, os pontos também pertencem a parábola

Passo 5

Usando uma ferramenta gráfica, pode-se esboçar o gráfico da parábola

A parábola é côncava para baixo, com valor máximo e ponto de máximo em Na imagem abaixo, a parábola é dada por uma curva preta mais escura.

Para vários valores de , forma plotadas as curvas das respectivas funções

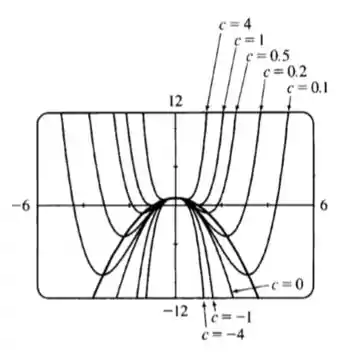
Observe que as funções que possuem ponto de mínimo realmente são aquelas com . Além disso, tanto os pontos de mínimo quanto os pontos de máximo encontram-se sobre a curva da parábola