Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.5 - Ex. 19
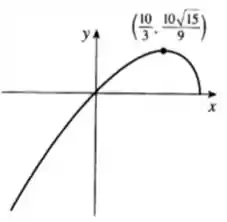
Use o roteiro dessa seção para esboçar a curva:
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a curva
E nosso objetivo é esboçar o gráfico de usando o roteiro dessa seção.
Lembra como fazemos isso?
O roteiro dessa seção pede para seguirmos um caminho para esboçar o gráfico de qualquer curva... vamos lembrar o que diz esse roteiro.
- 1° Domínio: Temos que primeiramente determinar o domínio da curva para sabermos onde nossa função é definida.
- 2° Intersecção com os eixos: aqui vamos fazer para saber quais valores de a curva intersecta o eixo e para saber onde a curva intersecta o eixo .
- 3° Simetria: Vamos verificar se para ver se a curva possui simetria par, se para ver se a curva possui simetria ímpar e se para ver se a função é periódica.
- 4° Assíntotas: Para verificar se a curva possui assíntotas horizontais, fazemos
- Já para verificar se a curva possui assíntotas verticais, temos que analisar a curva nos pontos de descontinuidade
- 5° Intervalos de crescimento e decrescimento: Vamos calcular a derivada da curva e analisando o intervalo onde , a função é crescente e quando a função é decrescente.
- 6° Máximos e mínimos: Para encontrar os pontos de máximos e mínimos, fazemos para obter os pontos críticos, calculamos e substituímos os pontos que encontramos... se , o ponto é de máximo e se o ponto é de mínimo.
- 7° Concavidade e pontos de inflexão: A concavidade da curva está relacionada com o sinal da segunda derivada... então se , a concavidade é voltada para cima e se a concavidade é voltada para baixo... quando temos um ponto de inflexão.
Bora começar!
Passo 2
Nosso primeiro passo é calcular o domínio da curva
Como nossa raiz não pode ser negativa, temos que:
Assim, o domínio é .
Passo 3
Agora precisamos achar os interceptos com os eixos...
Fazendo , temos
Temos que ou , ou ...
Dessa forma podemos concluir que o gráfico da função intercepta o eixo em dois pontos
Fazendo , temos
Então passa pela origem!
Tranquilo até aqui?
Passo 4
Agora vamos analisar a simetria da função...
Primeiro vamos ver se
Como a igualdade não bateu, a função não possui simetria par...
Para
Novamente a igualdade não bateu, então a função não possui nenhuma simetria.
Passo 5
Agora vamos analisar as assíntotas... começando pelas assíntotas horizontais:
Como a curva está definida apenas para menores que , podemos descartar a possibilidade de ter uma assíntota em
Se tende a , temos
Como o limite não convergiu para um valor, não temos assíntotas horizontais nesse gráfico.
E também não temos candidatos a assíntotas verticais, pois a função é contínua no seu domínio.
Show?
Passo 6
Agora vamos analisar os intervalos de crescimento e decrescimento...
Primeiro vamos calcular a primeira e a segunda derivada de
Pela regra do produto, temos
Aplicando a regra da cadeia na derivada de ...
Colocando tudo no mesmo denominador...
Calculando a segunda derivada pela regra do quociente...
Já calculamos a derivada de anteriormente...
Bacana?
Passo 7
Agora sim... analisando a inclinação de , temos que a curva é crescente quando , ou seja
E a curva decresce quando ...
Nesse caso, como a função cresce até e depois decresce, podemos afirmar que é um ponto de máximo global!
Como vimos no passo 3, a função tende a quando , então não temos mínimos nessa curva.
Estamos quase lá!
Passo 8
Por fim, vamos analisar os intervalos das concavidades e os pontos de inflexão...
Temos uma concavidade voltada para cima quando
E a concavidade para baixo quando
Perceba que em a função não está definida... dessa forma apenas o caso é válido. Isso significa que nossa curva possui apenas uma concavidade para baixo!
Se fizermos para encontrar os pontos de inflexão, vamos obter , que tambem está fora do nosso domínio, logo não tem um ponto de inflexão...
Passo 9
Por fim! Juntando tudo que encontramos até aqui, podemos esboçar a nossa curva como:
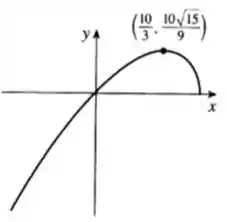
E aí! entendeu tudo? Responde Aí!
Resposta
