Descreva a mudança no gráfico de à medida que varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos de máximo e mínimo e os pontos de inflexão movem-se quando varia. Você deve também identificar qualquer valor intermediário de no qual o aspecto básico da curva mude.

A primeira coisa que podemos perceber na função é que em todas as aparições de seu expoente é par, logo, podemos concluir que nossa função terá simetria par .

Vamos escolher alguns valores de para plotar alguns gráficos...

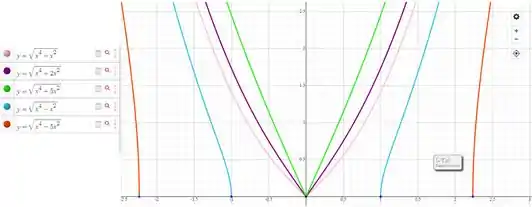
Para , , , e , temos

c ≥ 0 , é o único ponto interceptado no eixo . Quando , o eixo é interceptado em .

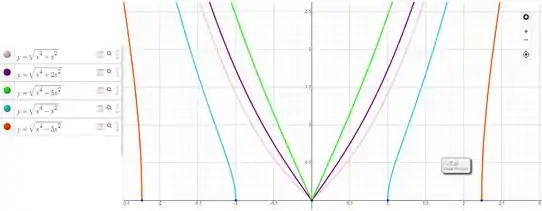
Já o eixo é interceptado em para pois . E quando , o eixo não é interceptado. Observamos também que a função é simétrica em relação ao eixo por ser uma função par.

Tranquilo até aqui?

Agora vamos analisar como e são afetadas pela variação de .

Para analisar os pontos de máximo e mínimo e de inflexão precisamos calcular as derivadas de .

Assim, temos que pela regra da cadeia ou usando uma ferramenta computacional.

Para

Para

Assim, verificamos que no ponto é o qual a função recebe a maior nítida variação quando aumenta. Existe um mínimo absoluto em para e não há outros máximos nem mínimos.

Além disso, quando a função só é definida se o conteúdo da raiz for maior ou igual a

Assim como vimos no passo 2

Show?

Calculando a derivada de segunda ordem usando uma ferramenta computacional...

Para

Assim, verificamos que a função tem concavidade para cima em e e concavidade para baixo em .

Existem pontos de inflexão em Quanto mais negativo fica, mais o ponto de inflexão se aproxima da origem. O único valor de transição é .

E aí! entendeu tudo? Responde Aí!