Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando aumenta.
3.
Passo 1
Queremos esboçar a curva que tem as equações paramétricas dadas. Bom, para fazer isso, vamos criar uma tabelinha de valores que relacionam , aí poderemos plotar esses pontos no gráfico.
Assim, quando , por exemplo, teremos e . Fazemos o mesmo para os outros valores de e montamos a seguinte tabela:

Show! Agora só precisamos colocar esses pontos em um gráfico e traçar uma linha unindo eles.
Passo 2
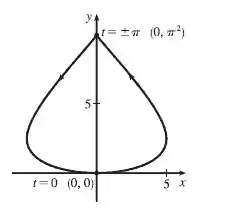
E o resultado é........ uma coxinha!
Resposta
Ei, a resposta está no passo a passo :)