O astrônomo Giovanni Cassini (1965-1712) estudou a família de curvas com equações polares
Para as quais e são números reais positivos. Essas curvas são chamadas ovas de Cassini, embora tenham formado oval apenas para certos valores de e . (Cassini pensou que essas curvas pudessem representar as orbitas planetárias melhor que as elipses de Kepler). Investigue a variedade de formatos que essas curvas podem ter. Em particular, como estão relacionados e quando a curva se divide em duas partes.
Passo 1
Não sei se você reparou, mas essa equação aí é uma equação polar implícita e a maioria dos programas gráficos não plota equações polares implícitas.
Isso significa que só pra conseguir começar a questão, a gente ainda vai ter que achar a equação explicita dessa bagaça aí.........
Repare que temos uma equação quadrática em , ou seja, organizando melhor
Então precisamos achar, a partir dessa expessão quadrática, o valor de em função de e também de e , que são as variáveis que queremos analisar o comportamento, afinal de contas.
Mesmo que pareça muuuuito complicado, como se trata de uma equação quadrática, podemos resolver usando a fórmula de baskara. Só que o nosso , na verdade é . Aí depois pra achar o valor de a gente ainda vai ter que tirar a raíz.
Vamos lá.
E pronto, é essa coisa bonita ai que temos que analisar o comportamento quando e variam.
Repare que nós temos QUATRO curvas!
As curvas porém são iguais, mas uma está na parte positiva e outra na parte negativa.
Passo 2
Vamos começar fazendo
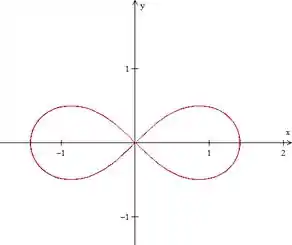
Taí nosso velho conhecido: o símbolo do infinito.
Passo 3
Agora vamos manter fixo e fazer variar.
- :
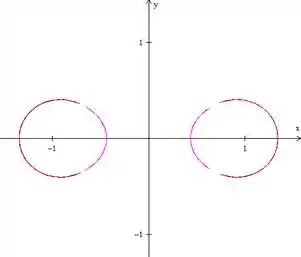
E a curva se divide em duas partes, formando duas bolinhas, sendo a parte vermelha a curva formada por
E a parte rosa a curva formada por
Beleza?
-:
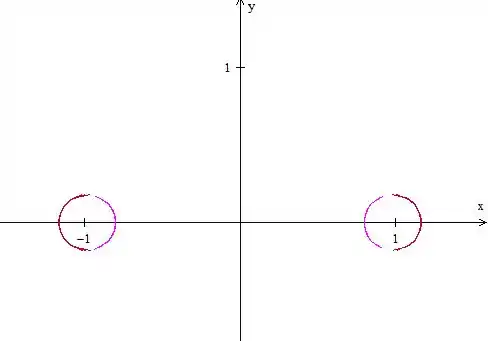
Ainda temos duas (que no caso são quatro né) curvas separadas, só que agora, mais afastadas uma da outra e mais redondinhas também, né?!
Assim, podemos notar que conforme diminui, a curva se divide em duas partes simétricas, que vão se tornando menores, mais afastadas uma da outra e mais redondas.
Passo 4
Agora vamos fazer aumentar.
- :
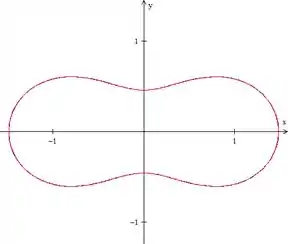
A curva aumenta de tamanho e se junta novamente em uma única curva fechada.
- :
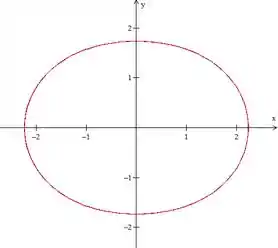
Aumentou mais ainda e está se tornando cada vez mais redonda.
Assim, conforme a gente aumenta o valor de , a curva volta a ser uma curva única fechada que tende a ficar cada vez mais redonda.
Passo 5
Agora vamos pegar um valor de fixo, por exemplo e fazer o variar.
-
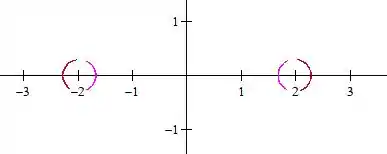
-
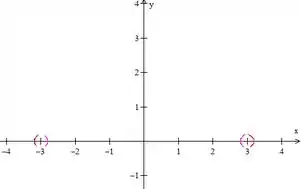
Aconteceu o mesmo que quando diminuímos o valor de mantendo fixo.
Passo 6
Agora vamos mudar completamente o valor de fixo. e vamos fazer
- :
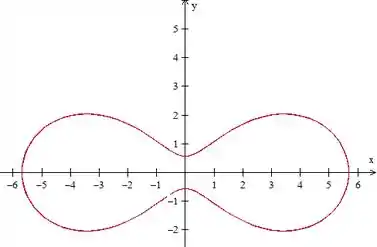
Olha o que que aconteceu com a curva!!! Ela mudou completamente seu formato!
Quer dizer, parece que a razão influencia no formato da curva.
Resposta
Ei, a resposta está no passo a passo :)