Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.3 - Ex. 1f

Calcule

∮ c f   d S

1.f

f x , y , z = x + y

E C é a curva obtida como interseção do semiplano

x = y

y ≥ 0

Com o paraboloide

z = x 2 + y 2

z ≤ 2

Passo 1

Oiii, existe um pequeno erro conceitual nessa questão. Usamos ds para designar uma seção de área, já dr usamos para uma seção de segmento de reta. Beleza? Queremos então calcular

∮ c f   d r

Um jeito de calcular isso é parametrizar nossa superfície r

r = σ t

d r = d σ t → σ ' t d t

Como estamos com um campo escalar, não podemos simplesmente plotar o vetor σ ' t d t na integral. Temos que transforma-lo em um escalar

v e t o r → e s c a l a r  

σ ' t d t → σ ' t d t

Então se parametrizarmos essa reta ficamos com

∫ t 0 t 1 f σ t ⋅ | σ ' t |   d t

Beleza!!! Vamos cair dentro \o/

Passo 2

Vamos preparar nossas funções para integral. Vamos parametrizar nossa função. Vamos achar uma parametrização bacana. Estamos na curva de interseção do paraboloide circular

z = x 2 + y 2

z ≤ 2

Com o plano

x = y

y ≥ 0

Logo podemos montar a seguinte parametrização

σ t = t , t , 2 t 2

Podemos perceber geograficamente que essa parametrização nos serve

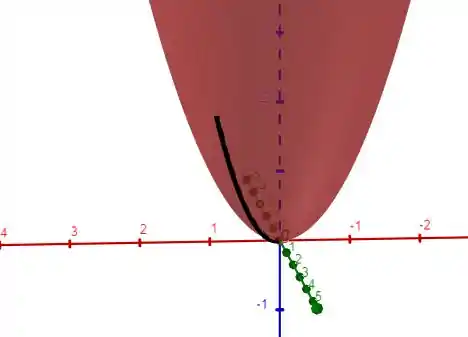
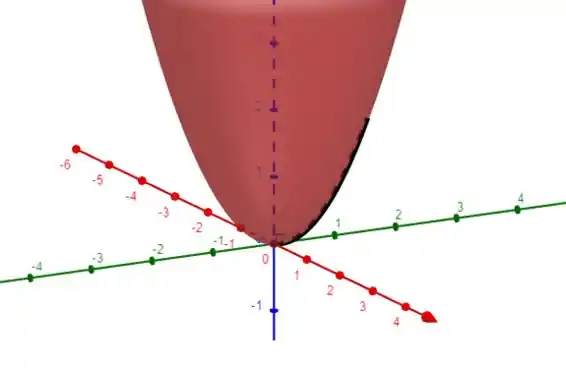
Passo 3

Vamos preparar nossa função escalar para a integral. Vamos parametrizar nossa função

f σ t → 2 t

Agora vamos calcular o modulo de σ ' t

σ ' t = 1 , 1 , 4 t

σ ' t = 1 2 + 1 2 + 4 t 2

= 2 + 16 t 2

Agora precisamos achar os intervalos de integração

σ t = t ,   t   ,   2 t 2

0,0 , 0 → 1 , 1 , 2

Para descobrir o ponto final basta substituir os valores na nossa parametrização

z = x 2 + y 2

z ≤ 2

2 = 2 t 2

t = 1

Com isso nosso intervalor é

t ∈ 0,1

Beleza, já temos tudo o que precisamos. Então nossa integração parametrizada fica

∫ t 0 t 1 f σ t ⋅ | σ ' t |   d t

∫ 0 1 2 t ⋅ 2 + 16 t 2 d t

Essa integração se resolver por substituição

u = 2 + 16 t 2

d u = 32 t   d t

Com isso nossa integral fica

∫ 0 1 2 t ⋅ 2 + 16 t 2 d t → 2 32 ∫ u d u

= 1 16 u 3 2 ⋅ 2 3

Vamos voltar de   u → t

= 1 24 2 + 16 t 2 3 2 0 1

= 1 24 18 3 2 - 2 3 2

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

∮ c f   d S = 1 24 18 3 2 - 2 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular as integrais curvilíneas. ∫ C x zd s , onde C é a interseção da esfera x 2 + y 2 + z 2 = 4 com o plano x = y .
Calcular as integrais curvilíneas. ∫ C y ( x - z ) , onde C é a interseção das superfícies x 2 + y 2 + z 2 = 9ex + z = 3 .
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 - z )d s , onde C é a parte da interseção das superfícies x 2 + y 2 + z 2 = 8 zez = 4
Calcular as integrais curvilíneas. ∫ C ( x + y + z )d s , onde C é o quadrado de vértices 1,0 , 1 ,1,1 , 1 ,0,1 , 1 ,( 0,0 , 1 ) .
Calcular as integrais curvilíneas. ∫ C ( x + y - 1 )d s , onde C é a parte da interseção das superfícies z = x 2 + y 2ey = 1 e que está abaixo do plano z = 5 .