Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.6 - Ex. 07
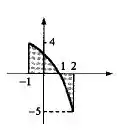
Desenhe o conjunto A dado e calcule a área:
A é o conjunto do plano limitado pela reta y = 0 e pelo gráfico de , com
.
Passo 1
Oi, pessoal! Para resolver esse problema, a gente tem que primeiro entender como é essa área, para depois achar os limites de integração e então resolver a integral definida.
Lembre-se: para desenhar a figura basta colocar os dados do problema, um de cada vez. Se for difícil enxergar o comportamento gráfico da função dada, teste alguns pontos do intervalo e faça o esboço. O conjunto se encontra sempre entre as funções dadas e marcá-lo no desenho ajuda a visualizar e calcular.
Vamos lá!
Passo 2
O problema pediu a área entre . Então vamos achar quanto vale a nossa função , nesses pontos:
Para , temos que
Para , temos que
Esboçando o gráfico, ficamos com
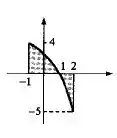
Lembrando que o problema pediu a área entre a função e o eixo , então temos uma região em que a área está acima do eixo e uma região em que ela está abaixo. Deste modo, vamos calcular cada região em separado.
Passo 3
Olhando para figura vemos que a região acima do eixo vai de , já a outra vai de .
Então a nossa integral fica assim,
Resolvendo a integral, temos
Resposta
