Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 8

Sejam F1 e F2 dois pontos distintos do plano e seja K a metadeda distância de F1 a F2. O lugar geométrico do Ponto P do plano tais que PF1 * PF2 = K² se chama lemniscata de focos F1 e F2.

  1. Tomando-se F1 = (-k,0) e F2=(k,0), determine a equação, em coordenadas cartesianas, de lemniscata.
  2. Passe para coordenadas polares a euqação obtida no item a) tomando para pólo a origem e x como eixo polar. Desenhe a curva.

Passo 1

No primeiro item, temos a seguinte situação:

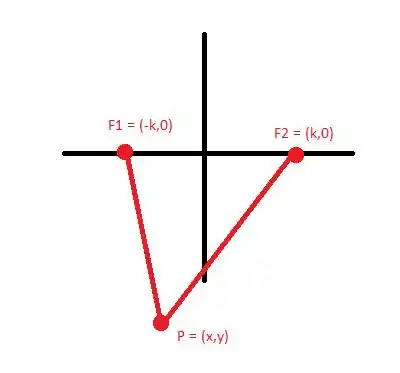
Onde P é um ponto qualquer.

Passo 2

Podemos calcular a distância entre os pontos:

Distância entre F1 e P → D 1 =   x + k 2 + y 2

Distância entre F2 e P → D 2 =   x - k 2 + y 2

Jogando na fórmula da lemniscata:

x + k 2 + y 2 x - k 2 + y 2 = k ²

x 2 - k 2 2 +   y 2 x - k 2 +   y 4 + y²(x+k)² = k4

x4 - 2x²k² + k4 + y4 + y²(x²+k²+x²+k²) = k4

Arrumando isso, chegaremos a:

x4 + y4 + 2y²x² = k²(2x²-2y²)

Note que, na primeira parcela, teremos um produto notável:

( x ² + y ² ) ² 2 x 2 - 2 y 2 = k²

Passo 3

Na letra b, o problema quer a equação em coordenadas polares:

Primeiramente, sabemos que:

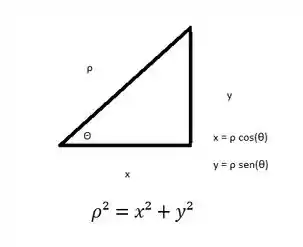
Logo, na primeira parcela:

( x ² + y ² ) ² 2 x 2 - 2 y 2 = ρ 2 2 2 ρ 2 c o s 2 θ - 2 ρ 2 s e n θ = ρ 2 2 c o s 2 θ - 2 s e n θ  

E finalmente, temos:

ρ 2 2 c o s 2 θ - 2 s e n θ = k ²

Agora basta desenhar a curva para os diferentes valores de k, utilizando uma tabela de pontos:

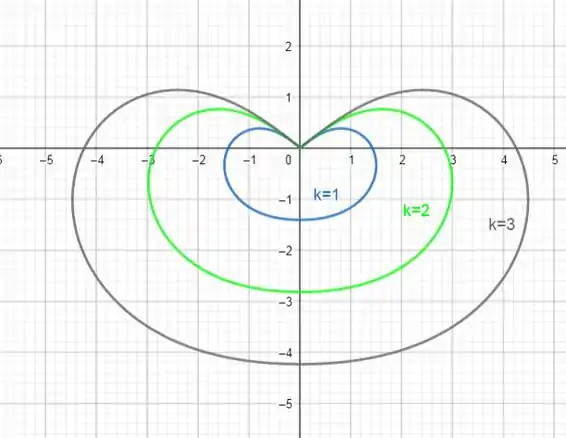
Resposta

  1. ( x ² + y ² ) ² 2 x 2 - 2 y 2 = k²
  2. ρ 2 2 c o s 2 θ - 2 s e n θ = k ²
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

22. Três partículas tendo massa 5,2 e 8 estão localizadas, respetivamente, nos pontos - 1 ,3 ,2 , - 1e5 ,2 . Ache o centro de massa sendo a distância medida em cm.
24. Três partículas, com igual massa, estão localizadas sobre o eixo x em pontos tendo coordenadas -4, 1 e 5, onde a distância é medida em metros. Ache as coordenadas do centro de massa do sistema.
26. O comprimento de uma barra é de 4m e a densidade linear da barra nem ponto a x m do extremo esquerdo é ( 3 x + 1 ) kg/m. Ache a massa total da barra e o centro de massa.
14) Ache o comprimento do arco da curva a y 2 = x 3 da origem ao ponto (4a, 8a)
O comprimento de uma barra é 8 m e a densidade linear da barra num ponto 2 x m do extremo esquerdo é 2 x + 1 kg/m . ache a massa total da barra e seu centro de massa.