Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 40

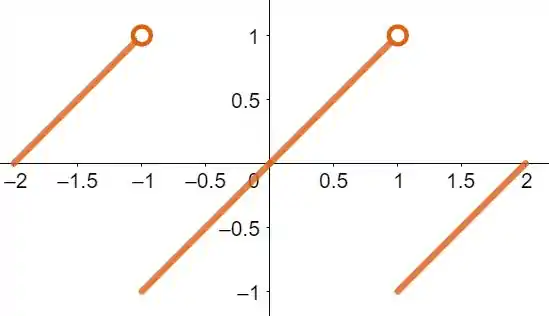
Desenhe os gráficos de f e f @ f .

f (x) = {[[x + 1 , - 2 <= x < 0],[x - 1 , 0 <= x <= 2]])

Passo 1

Para obter os gráficos das funções f e da composta de f com ela mesma será utilizado softwares. Entretanto, precisamos ter bastante cuidado quando tratamos da função composta f @ f . Imagem duas funções g ( x ) e h ( x ) . Se fizermos a composta g @ h , sabemos que:

  • O domínio de h ( x ) é o domínio de g @ h ;
  • A imagem de g ( x ) é a imagem de g @ h ;
  • A imagem de h ( x ) é o domínio de g ( x ) ;

É neste exato último ponto que devemos ter cuidado. Precisamos analisar o comportamento da imagem de f ( x ) , pois é ela quem será o domínio da própria f ( x ) (Confuso né? Imagina que a função interna vai ditar o domínio da mais externa).

Passo 2

Vamos começar por esboçar o gráfico da função f ( x ) .

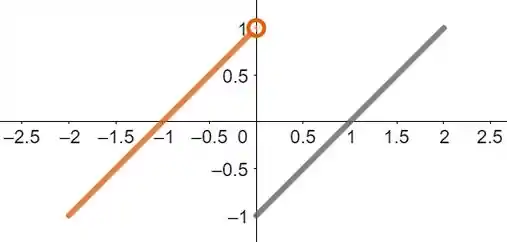
Detalhe para a bola aberta no final da reta x + 1 , pois o intervalo é aberto na extremidade x = 0 .

Passo 3

Antes de esboçarmos o gráfico de f @ f , vamos obtê-lo algebricamente. Vamos começar por obter no gráfico da função f ( x ) os intervalos tais que - 2 <= f (x) < 0 (a imagem da função vira o domínio da outra). Como pode ser observado facilmente, quando - 2 <= x < - 1 e 0 <= x < 1 , esta restrição é satisfeita. Sendo assim, quando - 2 <= x < - 1 teremos:

f (x + 1) = (x + 1) + 1 = x + 2

E quando 0 <= x < 1 teremos:

f (x - 1) = (x - 1) + 1 = x

Já nos intervalos - 1 <= x < 0 e 1 <= x <= 2 , temos 0 <= f (x) <= 2 . Consequentemente, para - 1 <= x < 0 teremos:

f (x + 1) = (x + 1) - 1 = x

E para 1 <= x <= 2 teremos:

f (x - 1) = (x - 1) - 1 = x - 2

Logo, podemos escrever a seguinte função f @ f :

f @ f = {[[x + 2 , - 2 <= x < - 1],[x , - 1 <= x < 0],[x , 0 <= x < 1],[x - 2 , 1 <= x <= 2]])

Passo 4

Se esboçarmos a função f @ f definida algebricamente no passo anterior, obtemos:

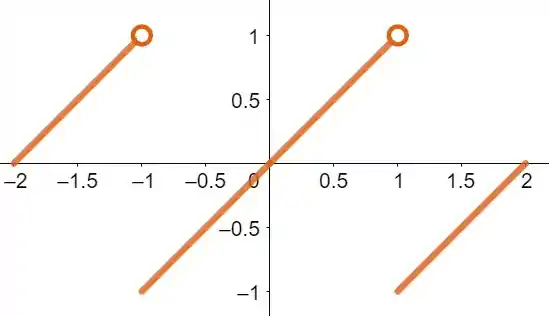
Resposta

Gráfico de f ( x ) :

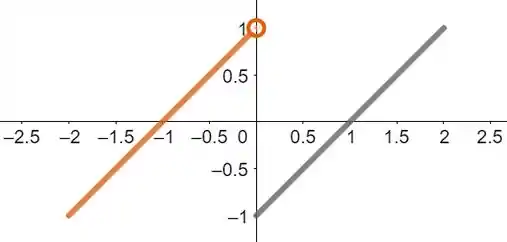
Gráfico de f @ f

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estão definidas as funções f e g . Defina a seguinte função e determine o domínio da função composta: g ∘ f f x = x - 2 ; g x = x 2 - 2
Estão definidas as funções f e g . Defina a seguinte função e determine o domínio da função composta: f ∘ g f x = x - 2 ; g x = x + 7
Estão definidas as funções f e g . Defina a seguinte função e determine o domínio da função composta: f ∘ g f x = x ; g x = x 2 + 1
Estão definidas as funções f e g . Defina a seguinte função e determine o domínio da função composta: f ∘ g f x = x - 5 ; g x = x 2 - 1
Estão definidas as funções f e g . Defina a seguinte função e determine o domínio da função composta: g ∘ f f x = 3 - 2 x ; g x = 6 - 3 x