Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 45
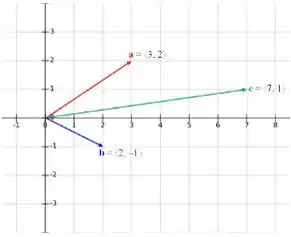
- Desenhe os vetores
- Mostre, por um esboço, que existem escalares e tais que
- Use o esboço para estimar os valores de e .
- Determine os valores exatos de e .
Passo 1
- Desenhando os vetores
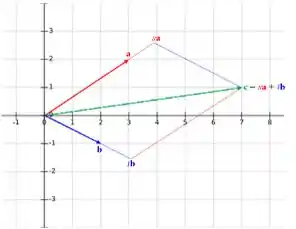
- Pelo desenho, podemos ver que é algum escalar múltiplo do vetor , e é um escalar múltiplo do vetor . E com eles podemos formar um paralelogramo que tem com diagonal, então , para algum escalar e
- Do esboço na parte (b), parece que pois parece ser um terço maior que . Da mesma forma, parece que , porque também parece ser maior que .
- Agora vamos calcular os valores exatos de e :
Passo 2
Passo 3
Se de fato e , então
Como podemos ver, esse não é exatamente o vetor , mas está bem próximo e tudo bem, pois aqui estamos apenas fazendo uma aproximação. O valor exato calcularemos no próximo item.
Passo 4
Então, e .
Resposta
(c)
(d)
Exercícios de Livros Relacionados
Determinar o vetor v → nos seguintes casos: v → é ortogonal ao eixo O z , v → = 8 , forma ângulo de 30 ° com o vetor i → e ângulo obtuso com j → .
Determinar o vetor v → nos seguintes casos: v → é ortogonal ao eixo O x , v → = 2 , forma ângulo de 60 ° com o vetor j → e ângulo agudo com k → .
Mostrar que existe vetor cujos ângulos diretores são 30 ° , 90 ° e 60 ° , respectivamente, e determinar aquele que tem módulo 10 .
Para cada um dos pares de vetores u → e v → , encontrar a projeção ortogonal de v → sobre u → e decompor v → como soma de v → 1 com v → 2 , sendo v → 1 | | u → e v → 2 ⊥ u → . u → = 1,2 , - 2 e v → =
Sejam A 2,1 , 3 , B m , 3,5 e C 0,4 , 1 vértices de um triângulo (Figura 2.18 ) responda:Mostrar que A H - ⊥ B C - .