Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 2.Problemas Propostos - Ex. 43d

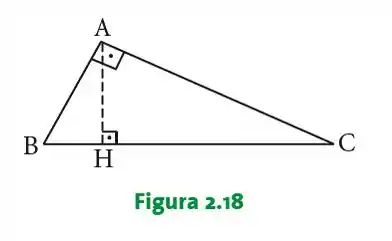
Sejam A 2,1 , 3 , B m , 3,5 e C 0,4 , 1 vértices de um triângulo (Figura 2.18 ) responda:

Mostrar que A H - ⊥ B C - .

Passo 1

Para mostrar que A H - ⊥ B C - podemos usar que sabemos que se dois vetores são ortogonais, seu produto escalar deve ser igual a zero, vamos então calcular o produto escalar e ver se ele é igual a zero.

Primeiro vamos achar os vetores A H - e B C - , usando o ponto H que achamos na letra c):

A H - = H - A = 51 26 , 87 26 , 94 26 - 2,1 , 3 = 51 26 - 2 , 87 26 - 1 , 94 26 - 3 =

= 51 - 52 26 , 87 - 26 26 , 94 - 78 26 = - 1 26 , 61 26 , 16 26

B C - = C - B = 0,4 , 1 - 3,3 , 5 = 0 - 3,4 - 3,1 - 5 = - 3,1 , - 4

Passo 2

Pronto, agora é só calcular o produto escalar:

A H - ⋅ B C - = - 1 26 , 61 26 , 16 26 ⋅ - 3,1 , - 4 = - 1 26 ⋅ - 3 + 61 26 ⋅ 1 + 16 26 ⋅ - 4 =

= 3 26 + 61 26 - 64 26 = 0

Pronto, o produto escalar A H - ⋅ B C - deu zero, então mostramos que A H - ⊥ B C - .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.Prove que A - u → + v → = A - ( u → - v → )
9.Prove que A + u → + v → + w → = A + u → + ( v → + w → )
7.Determine a relação entre u → ev → , sabendo que, para um dado ponto A , A + u → + v → = A
6.Prove que A + u → = B + v → ⇒ u → = A B → + v →
Prove que, se P = A - u → , então A B → + u → = P B →