Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 42
- Encontre os vetores unitários que são paralelos à curva no ponto .
- Encontre os vetores unitários que são perpendiculares à reta tangente.
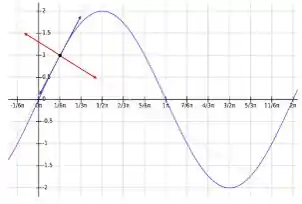
- Esboce a curva e os vetores nas partes (a) e (b), todos começando em .
Passo 1
- Queremos encontrar os vetores unitários que são paralelos à curva no ponto .
- Queremos encontrar os vetores unitários que são perpendiculares à reta tangente. A inclinação da reta tangente é , como vimos no item (a). Para uma reta ser perpendicular a outra, sabemos que a multiplicação entre as inclinações deve ser igual a . Então:
- A curva azul é o gráfico de , a reta roxa é o vetor unitário e a reta vermelha é a perpendicular
Para isso, vamos derivar nossa curva, pois assim encontramos a inclinação da reta que estamos procurando:
Como estamos falando do ponto , vamos trocar :
Então nesse ponto, nossa inclinação é . A equação da reta paralela tem a mesma inclinação, portanto será:
A inclinação de uma reta pode ser dada por , então
satisfaz essa equação.
Agora vamos calcular o módulo do vetor que encontramos:
Para que esse vetor seja unitário, precisamos dividir suas componentes pelo seu módulo, então:
Passo 2
Então a equação de uma reta perpendicular, porém não passando pelo ponto é:
Lembre-se que a inclinação de uma reta pode ser interpretada como , então encontramos o par .
Show! Agora vamos encontrar o módulo desse vetor:
Para que nosso vetor seja unitário, precisamos dividí-lo pelo seu módulo:
Passo 3
Resposta
36. (a)
(b)