Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.1 - Ex. 72
Determine se a sequência está aumentando, diminuindo ou não monotônico.A sequência é limitada?
Passo 1
Tudo certo, pessoal? Bora resolver essa questão:
A primeira parte que precisamos definir é sobre o comportamento da sequência, ou seja, se ela está aumentando (crescente), diminuindo (decrescente) ou se seu comportamento é não monotônico.
Como sabemos uma sequência não monotônica é uma sequência em que não há uma tendência consistente de aumento ou diminuição ao longo do tempo. Nela, os elementos podem alternar entre aumentos e diminuições, ou podem permanecer relativamente constantes em certos períodos, sem uma direção clara.
Galerinha, uma função é dita monotônica se e somente se manter o mesmo sinal para todo . Além disso, a função pode ser crescente se para todo e pode ser decrescente se para todo . Podemos tomar nossa sequência como uma função contínua para fazermos essa análise.
Outra forma de entender se uma função é crescente ou decrescente é compararmos os termos e o seu sucessor . A sequência pode ser crescente se para todo e pode ser decrescente se para todo .
No nosso caso, como sabemos bem o comportamento de e é facil de derivar, usaremos a estratégia de analisar o sinal da derivada.
A segunda pergunta que a questão nos trás é se a sequência é limitada, ou seja, se ela é limitada tanto superiormente quanto inferiormente, ou seja, valores de máximo e mínimos que a sequência não ultrapassa.
Vamos analisar passo a passo, então!
Passo 2
Vamos analisar o comportamento da função quanto ao crescimento ou decrescimento. No nosso caso, temos uma sequência muito conhecida. Vamos analisá-la como se fosse uma função contínua para fins de simplificação:
Analisamos o sinal da derivada para entendermos se ela cresce ou decresce. Para isso, vamos calcular a primeira derivada dela:
Nesse caso, a derivada assume tanto sinal negativo quanto sinal positivo devido ao comportamento periódico da função conforme os valores de variam. Logo, ela não é monotônica.
Relembrando o gráfico de :
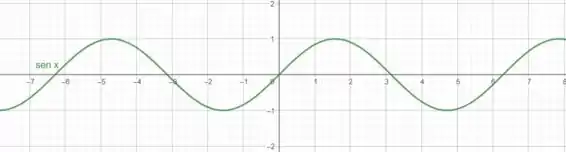
O fato de termos só espelhará nosso gráfico, mas ela continuará oscilando e sendo não monotônica, então é não monotônica
Passo 3
Agora vamos analisar a segunda parte da sequência e entender se ela é limitada. Vejamos o gráfico de .
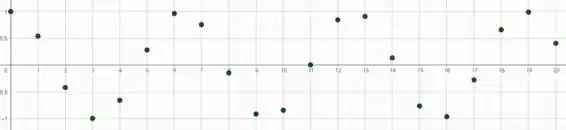
Essa sequência é limitada porque o máximo valor que ela assume é e o mínimo é , como podemos ver pelo seu gráfico.
Então:
Resposta
A sequência é limitada e não monotônica.