Determinar todos os intervalos de um número que satisfaçam as desigualdades abaixo. Fazer a representação gráfica.
e)
Passo 1
Essa questão é um pouquinho grande, mas bem simples de entender. É necessário analisar os casos onde as soluções são cabíveis! Calma jovem gafanhoto, se liga que você vai entender já já o que estamos falando!
Primeiro caso:
Solução para o primeiro caso:
Segundo caso:
Solução segundo caso:
Solução final:
Inicialmente estuda - se todas as possibilidades para valor de e faz – se o intervalo de convergência desses valores. Depois de feito tudo isso, fazemos a intersecção dos valores encontrados, por isso a solução final. Okay?
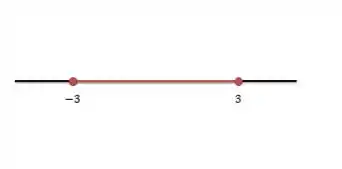
A representação gráfica será: