Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.7 - Ex. 15

Determinar o volume do sólido de revolução gerado pela rotação das regiões indicadas, ao redor dos eixos dados.

y = x + x 2 e y = x 2 - 1 ; ao redor do eixo y = 1

Passo 1

Inicialmente, é importante fazer um esboço das duas curvas. Se liga nessa ilustração onde a vermelha representa y = x + x 2 e a azul y = x 2 - 1 :

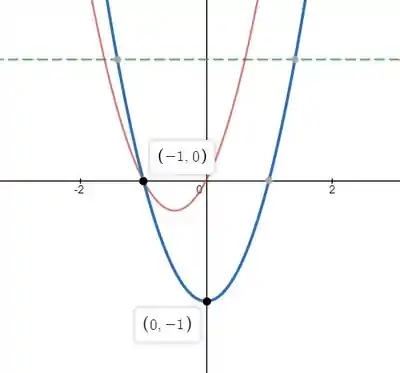
Para acharmos o ponto de interseção, vamos fazer assim:

y = x + x 2 y = x 2 - 1

Substituindo a primeira na segunda:

x + x 2 = x 2 - 1

Logo,

x = - 1

Voltando na primeira equação:

y = - 1 + 1 → y = 0

Portanto, teremos o seguinte ponto:

- 1,0

Passo 2

Como estamos rotacionando em torno do eixo y vamos usar a seguinte expressão:

V = π ∫ a b f x - 1 2 d x

Agora vamos ver como ficam as funções que definem as curvas. Para curva vermelha:

y = x + x 2

Assim,

f x = x + x 2

Já para curva azul:

y = x 2 - 1

Logo,

g x = x 2 - 1

Passo 3

Então o volume vai ficar o seguinte:

V = π ∫ - 1 0 g x - 1 2 d x - π ∫ - 1 0 f x - 1 2 d x

Assim,

V = π ∫ - 1 0 x 2 - 1 - 1 2 d x - π ∫ - 1 0 x + x 2 - 1 2 d x

Juntando as integrais:

V = π ∫ - 1 0 x 2 - 2 2 - x + x 2 - 1 2 d x

Repare que agora temos uma diferença de quadrado. Logo,

V = π ∫ - 1 0 2 x 2 + x - 3 - x - 1 d x

Fazendo a distributiva:

V = π ∫ - 1 0 [ - 2 x 3 - 3 x 2 + 2 x + 3 ] d x

Não esquece: ∫ x n d x   = x n + 1 n + 1 + c   quando   n   ≠ - 1

Passo 4

Integrando:

V = π - 2 x 4 4 - 3 x 3 3 + 2 x 2 2 + 3 x - 1 0

Aplicando entre esses pontos:

V = π - 2 × 0 4 - 3 × 0 3 + 2 × 0 2 + 3 × 0 - - 2 × - 1 4 4 - 3 × - 1 3 3 + 2 × - 1 2 2 + 3 × - 1

Logo,

V = π [ 0 - 1 2 + 1 + 1 - 3 ]

Portanto,

V = 3 π 2

Resposta

V = 3 π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Determine o volume do sólido obtido com a rotação da região limitada pela parábola y = x 2 e pela reta y = 1 em torno Da reta y = 1 .Da reta y = 2 .Da reta y = - 1 .
Determine o volume do sólido obtido com a rotação da região limitada pela parábola y = x 2 e pela reta y = 1 em torno Da reta y = 1 .Da reta y = 2 .Da reta y = - 1 .
Determine o volume do sólido obtido com a rotação da região limitada por y = 2 x , y = 0 e pelas retas x = 1 em torno Da reta x = 1 .Da reta x = 2 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /