Determine o volume do sólido obtido com a rotação de cada região em torno do eixo dado. A região é a região, no segundo quadrante, limitada acima pela curva , abaixo pelo eixo e à esquerda pela reta em torno da reta .

Vamos começar por esboçar a nossa região limitada pelas curvas.

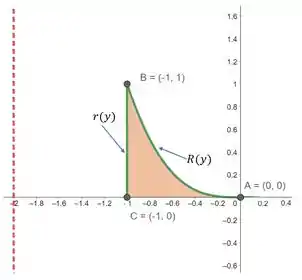
Em destaque temos a região limitada pelas curvas. Temos que descobrir agora quem são essas funções que definem os raios externos e interno.

Inicialmente, iremos determinar as curvas em relação ao nosso eixo . Posteriormente, faremos uma translação horizontal da função. Começando pela curva , ela é a curva que limita nossa região à direita. Segundo o enunciado da própria questão, ela é:

Isolando o na função, obtemos:

Já para a curva , é a reta que limita a nossa região à esquerda. Pelo enunciado, sabemos que:

Agora, temos que escrever as curvas e em relação ao nosso eixo de rotação, a reta . Para isto, basta verificar que o eixo corresponde à reta transladada para a direita em duas unidades. Portanto, precisamos transladar as nossas curvas e para a direita em duas unidades. Desta forma, vamos obter as seguintes funções

Agora já obtivemos as curvas em relação ao eixo , nos falta apenas determinar os limites de integração. Para isto, basta responder a seguinte pergunta: qual o menor e o maior valor de na nossa região? Eles são 0 e 1, respectivamente. Agora sim, vamos calcular a nossa integral!