Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.4 - Ex. 18

Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado.Se você tiver um programa gráfico, poderá traçar o gráfico da curva para verificar a sua aparência.

x = 1 3 y 3 2 - y 1 2 ,         1 ≤ y ≤ 3 ;         e i x o   y

Passo 1

Para essa questão é importante visualizarmos o gráfico da curva. Veja:

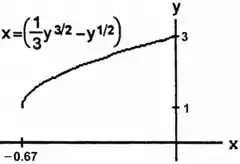
Para o intervalo definido temos que x = 1 3 y 3 2 - y 1 2 ≤ 0 ,   logo podemos escrever que

x =   - 1 3 y 3 2 - y 1 2 , a fim de se obter um resultado positivo para a área.

Passo 2

Por definição temos que se a x = g y ≥ 0   é continuamente derivável em [ c , d ] , a área da superfície gerada pela rotação da curva x = g ( y ) em torno do eixo y é:

S = ∫ c d 2 π g ( y ) 1 + g ' y 2   d y

Assim, temos que:

S = - ∫ 1 3 2 π   1 3 y 3 2 - y 1 2 1 + 1 2 ( y 1 2 - y - 1 2 ) ) 2       d y =

= - 2 π ∫ 1 3 1 3 y 3 2 - y 1 2 1 + 1 4 y - 2 + y - 1   d y =  

= - 2 π ∫ 1 3 1 3 y 3 2 - y 1 2 1 4 y + 2 + y - 1   d y =  

= - 2 π ∫ 1 3 1 3 y 3 2 - y 1 2 y 1 2 + y - 1 2 2 2     d y = - π ∫ 1 3 y 1 2 1 3 y   - 1 y 1 2 + 1 y 1 2     d y =      

= - π ∫ 1 3 1 3 y   - 1 y + 1     d y =   - π ∫ 1 3 1 3 y 2 - 2 3 y - 1 d y

Passo 3

Integrando, temos:

- π ∫ 1 3 1 3 y 2 - 2 3 y - 1 d y = - π y 3 9 - y 2 3 - y 3 1

Lembre-se que a integração de um polinômio é dada por:

∫ x n   d x = x n + 1 n + 1

Passo 4

Por fim, aplicamos os limites de integração e calculamos a área:

S =   - π y 3 9 - y 2 3 - y 3 1 = - π 3 - 3 - 3 - 1 9 - 1 3 - 1 = - π 9 - 18 - 1 + 3 = 16 π 9

Relembrando que de forma genérica a aplicação dos limites de integração ele é feito da seguinte maneira:

∫ a b f x d x = F b - F ( a )

Ou seja, após integrar de forma genérica você irá substituir os limites de integração ( a e b) nesse resultado obtido, respeitando a ordem de o limite superior aplicado na função menos o limite inferior aplicado na função.

Resposta

16 π 9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a área da superfície obtida pela rotação da curva em torno do eixo x x = 1 + 2 y 2 , 1 ≤ y ≤ 2
Calcule a área da superfície obtida pela rotação da curva em torno do eixo x x = 1 3 y 2 + 2 3 2 , 1 ≤ y ≤ 2
Use a regra de Simpson com n = 10 para aproximar a área da superfície obtida pela rotação da curva em torno do eixo x . Compare o seu resultado com o valor da integral obtido em sua calculadora y = se
A curva dada é girada em torno do eixo y . Calcule a área da superfície resultante y = x 3 , 1 ≤ y ≤ 2
Use a regra de Simpson com n = 10 para aproximar a área da superfície obtida pela rotação da curva em torno do eixo x . Compare o seu resultado com o valor da integral obtido em sua calculadora y = x