Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 49
- Determine a derivada da função dada
- Faça os gráficos de e lado a lado empregando planos coordenados diferentes e responda às questões a seguir.
- Para que valores de x, se for o caso, é positivo? E nulo? E negativo?
- Existe algum intervalo de valores de x em que a função cresce quando x aumenta? Ou diminui à medida que x aumenta? Como isso está relacionado com o que foi visto no item ( c )?
Passo 1
Primeiro calculamos a derivada de
Passo 2
Item (b)
Gráfico de
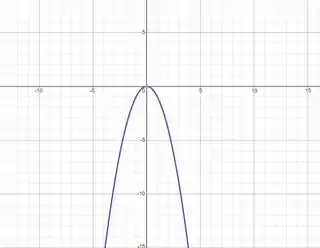
Gráfico de
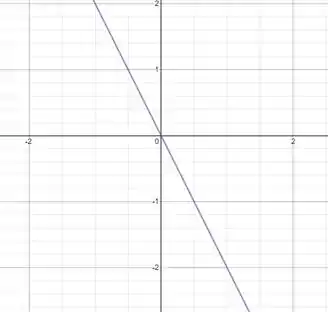
Passo 3
Item (c)
Passo 4
Para os valores de menores que zero, a função é crescente, o que indica um coeficiente angular positivo para a reta tangente. Já para os valores de maiores que zero, a função é decrescente, por isso a derivada é negativa.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se f é contínua em x 1 ; (c) calcule f ´ _ _ ( x 1 ) e f ´ + x 1 , se existirem, (d) determine se f é