Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 48
Em que pontos do domínio a função parece ser
- derivável?
- contínua, mas não derivável?
- nem contínua, nem derivável?
Passo 1
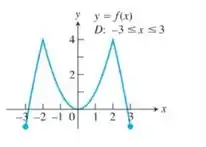
Primeiro, podemos notar que a função é definida por partes, logo, pode não ser derivável em todos os pontos.
Passo 2
A função parece contínua em todos os pontos do domínio, mas não parece ser derivável nos pontos em comum das partes. Logo, parece ser derivável no seguinte conjunto
Observando as retas tangentes às partes, percebemos que para e para
A função é contínua mas não parece derivável.
Item (c)
Nenhum ponto
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d