Determine o dominio:
Passo 1
Para encontrar o domínio dessa função é importante lembrar que o domíni0 de uma função é justamente o intervalo da variável onde ela existe. Como não existe raiz quadrada de número negativo, então devemos estudar o sinal da função.
Por produtos notaveis, temos que a difereça de dois quadrado pode ser fatorado pelo produto da soma pela diferença, ou seja:
Então, as raízes são e .
Passo 2
Assim, podemos construir uma tabela estudando o sinal de cada termo:
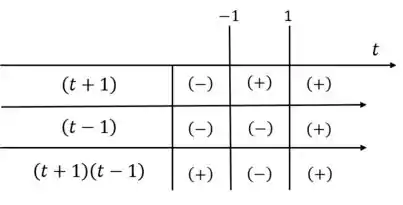
Vemos que a raiz só admite valores de menores ou iguais a ou maiores ou iguais a pois nesses intervalos não teremos valores negativos para .
Logo, o domínio é dado por: