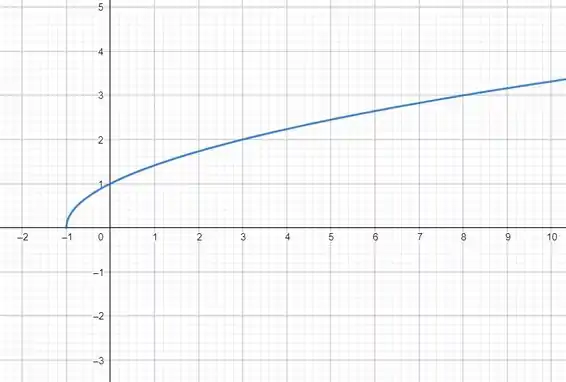
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Agora temos uma função um pouco mais peculiar do que as anteriores, vamos analisar cada coisa de uma vez. Começando pelo domínio, depois a imagem e por último vamos ver o gráfico da função.
Passo 2
Nada de novo sobre descobrir o domínio de uma função que tenha uma raiz, né? Sabemos que o que está dentro da raiz tem que ser maior ou igual a , ou seja:
E daí temos que:
E então o nosso domínio fica
Passo 3
Quanto à nossa imagem, vamos ficar com todos os valores não negativos, pois é isso que pode resultar de uma raiz quadrada. Podemos encontrar isso analiticamente também:
Agora é só tirar a raiz dos dois lados:
E isso do lado esquerdo da equação é a nossa ! Ou seja:
Que é o que já esperávamos! Nossa imagem também já tá na mão:
Passo 4
Agora vamos ao gráfico da . Pense que temos a metade de uma parábola deitada. É como se tivéssemos a função , mas só pegando a parte positiva do gráfico:
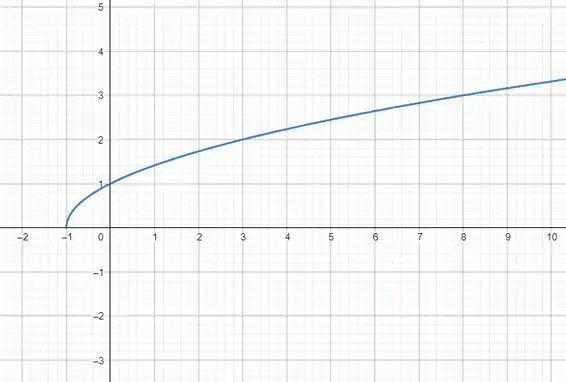
Resposta
Domínio:
Imagem: