Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 2
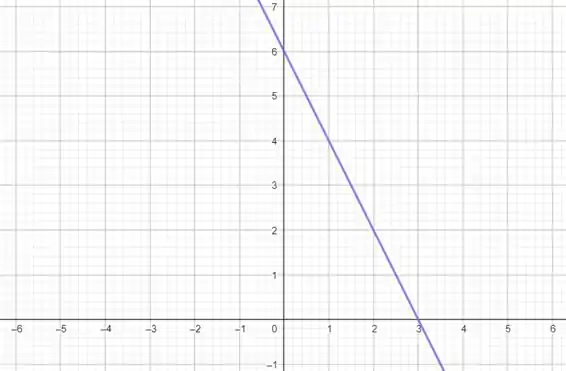
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
A questão quer o domínio, a imagem e o gráfico da função. Vamos começar pelo gráfico e daí já fica fácil de determinar o domínio e a imagem dela.
Passo 2
Temos um polinômio do 1º grau. O gráfico disse vai ser uma reta! Podemos esboçar o gráfico dessa função achando dois pontos que satisfazem a função e depois é só desenhar a reta que passa pelos dois pontos!
Vamos encontrar os dois pontos fazendo e :
Temos os dois pontos e
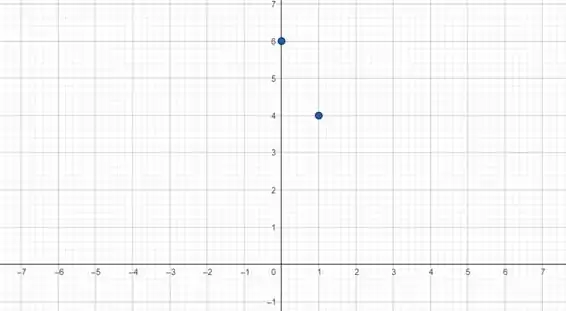
Agora só precisamos de uma reta que passe por esses dois pontos:
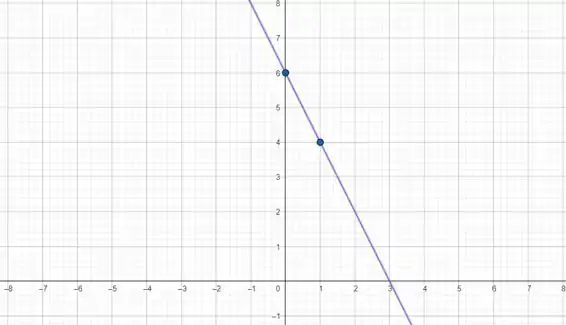
Essa reta é o gráfico da nossa função!
Passo 3
Uma reta está definida para todos os valores e e pode resultar em qualquer valor de , então tanto o conjunto do domínio quanto o da imagem será
Resposta
Domínio:
Imagem:
