Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 20

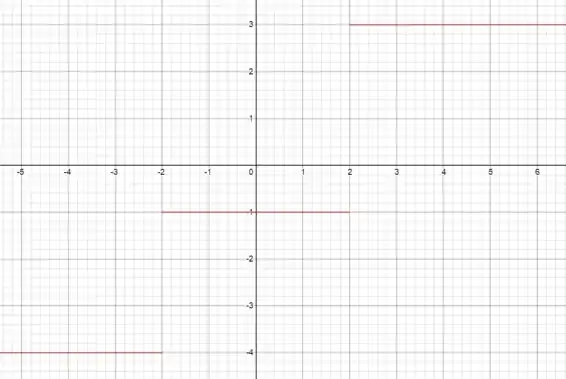
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.

h x = - 4 ,   s e   x < - 2 - 1 ,   s e - 2 ≤ x ≤ 2 3 ,   s e   2 < x

Passo 1

A nossa função é uma função condicional de três intervalos! E em cada intervalo ela se comporta como uma função constante, daí já sabemos que nossa imagem será a união de todos os valores constantes da função. Daí ficamos com a nossa imagem: { - 4 ,   - 1 ,   3 }

Passo 2

O domínio também é tranquilo de definir, é só ver para que valores de x está definida a nossa função. Ela está definida naqueles 3 intervalos: - ∞ ,   - 2 ,   - 2 ,   2 ,   2 ,   + ∞ . Se fizermos a união desses 3 conjuntos teremos o domínio da nossa função! E repare que se fizermos a união desses conjuntos ficaremos com - ∞ ,   + ∞ , que é o nosso domínio.

Passo 3

Agora ao gráfico. Sem mistério, a função vai ser constante igual a - 4 de - ∞ até   - 2 . De - 2 até 2 elai vai ser - 1 e para todos os valores de x > 2 , a função terá valor 3 . No plano cartesiano:

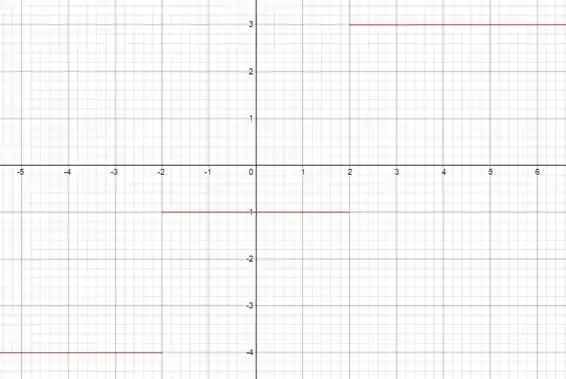
Resposta

Domínio: - ∞ ,   + ∞

Imagem: { - 4 ,   - 1 ,   3 }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que f e g são ambas funções ímpares, definidas em toda a reta real. A função f g (se estiver definida) é par?
Determine o maior intervalo em que a função f ( x ) = | x - 2 | + 1 é crescente.
Determine (a) o domínio e (b) a imagem de y= - 2 + 1 - x
Determine o maior intervalo em que a função R ( x ) = 2 x - 1 é crescente.
Determine (a) o domínio e (b) a imagem de y=| x | - 2