Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 13
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Vamo lá, a questão quer o domínio, a imagem e o gráfico da função. Vamos fazer um de cada vez nessa mesma ordem que tudo sai no fluxo.
Passo 2
Pra determinar o domínio não tem stress nenhum, né? Nada de raiz, nada de no denominador então o nosso domínio será:
Passo 3
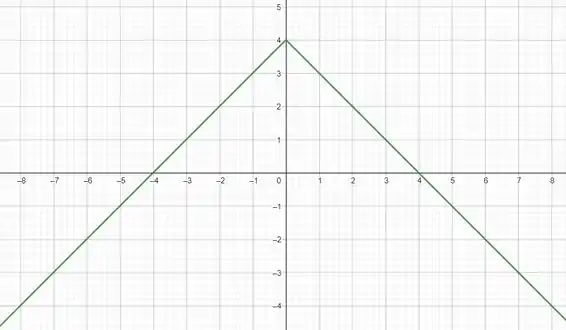
Batendo o olho na função, já dá pra ver que e são inversamente proporcionais e ainda mais, podemos dizer que a função tem um “teto” já que estamos em função do módulo de . Vamos achar o ponto onde a função tem seu maior valor. Como o maior valor de é em , vamos fazer :
Então nossa função terá a imagem:
Passo 4
E seu gráfico vai ficar assim:
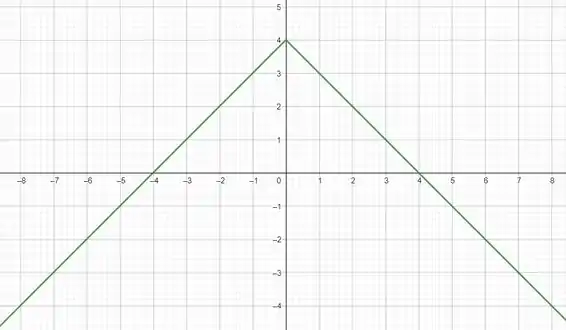
Resposta
Domínio:
Imagem:
Exercícios de Livros Relacionados
Encontre o domínio e faça o gráfico das funções nos Exercícios 15-20.15. f x = 5 - 2 x
14. Considere o ponto ( x , y ) que está no gráfico de y = x - 3 . Sendo L a distância entre os pontos x , y e ( 4,0 ) , represente L em função de x .
Nos exercícios 7 e 8 quais gráficos são de funções de x e quais não são? Justifique suas respostas.8. a. Para um gráfico ser de em função de x , cada valor de x só pode corresponder a um valor de y .
Encontre o domínio e faça o gráfico das funções nos Exercícios 15-20.18. g x = - x
Para os Exercícios 1-6, encontre o domínio e a imagem de cada função.3. F x = 5 x + 10 O domínio da função vai ser o conjunto de todos os números que gente pode colocar na função e que não vai dar pro