Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 26

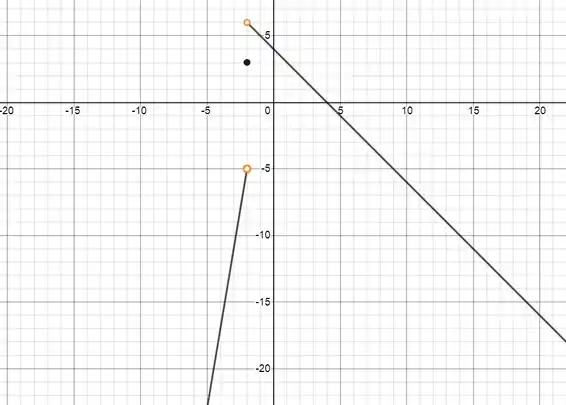
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.

Passo 1

Vamos fazer como a última questão, primeiro plotar o gráfico e depois analisar o domínio e a imagem da função. De intervalo em intervalo vamos plotando como ela se comporta, começando pelo primeiro intervalo que temos a equação da reta

Vamos achar 2 pontos que satisfaçam equação e daí podemos encontrar o gráfico da reta que liga os dois pontos. Vamos fazer e :

Agora é só ligar os dois pontos e que encontramos e teremos nossa reta:

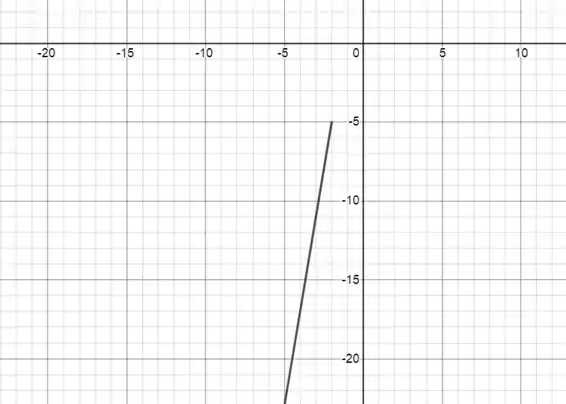
Passo 2

Agora vamos para o intervalo intermediário, que é um ponto: . Adicionando esse ponto ao nosso gráfico anterior:

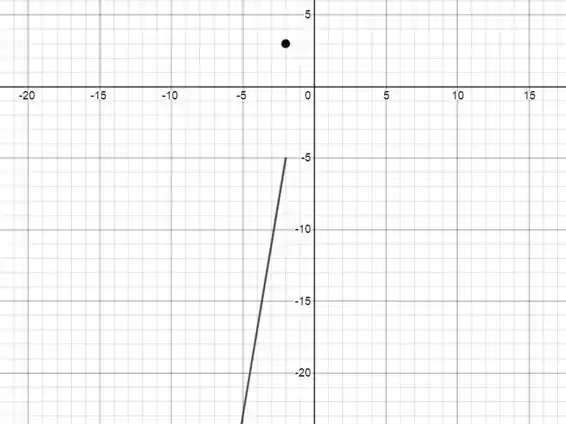
Passo 3

Vamos agora para a última parte da nossa função condicional: para .

Isso é a equação de uma reta com coeficiente angular e cruza o eixo no ponto . Daí temos a última parte que faltava para completar o nosso gráfico:

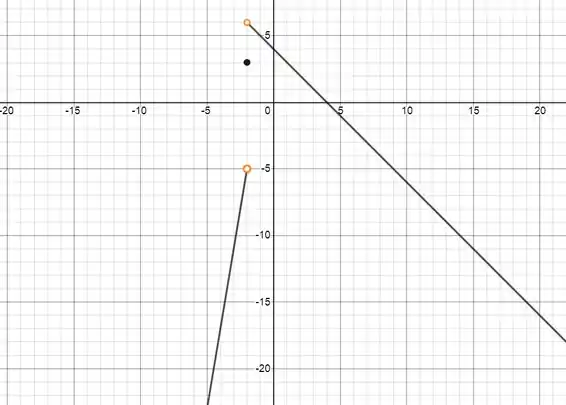
Passo 4

Agora fica tranquilo de determinar o domínio e a imagem né? O domínio é todo o conjunto dos reais, já que não temos nenhuma restrição em . Já a imagem da função é limitada até aquele valor no topo da reta da esquerda que é . Repare que a bolinha está aberta, então aquele valor não pertence à imagem.