Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 23
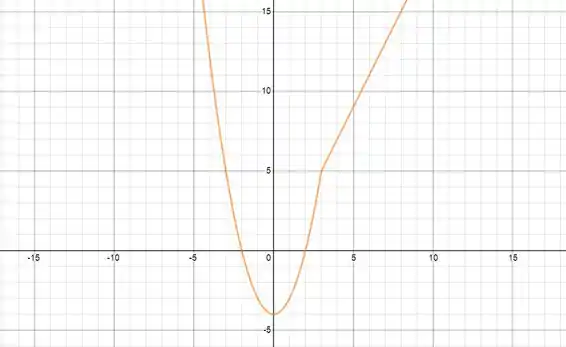
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Vamos começar definindo o domínio. As condições incluem todos os números reais e não temos nenhuma divisão por , nenhuma raiz quadrada, nada disso, então o domínio de será .
Passo 2
Para a imagem dessa função, precisamos ser um pouco cuidadosos. Vamos ter que ver como ficam as coisas para os valores de pois a imagem de uma função quadrática é restrita.
Sabemos que:
Subtraindo de ambos os lados:
Ou seja:
Essa será a restrição da nossa imagem. Ou seja:
Não precisamos nos preocupar com que restrição a 2ª condição da função impõe, pois a partir do ponto que ela é definida ela já é igual a , que já está dentro da imagem definida pela 1ª equação. E não precisamos nos preocupar com nenhum outro valor da 2ª equação porque ela é uma reta crescente, seu menor valor vai ser em
Passo 3
O gráfico será uma parábola deslocada em unidades no eixo até A partir de , a função se comporta como uma reta e cresce até o . Desse jeito:
Resposta
Domínio:
Imagem:
