Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 25
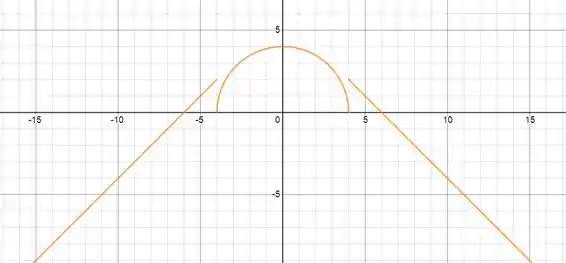
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Vamos seguir um caminho inverso nessa função: primeiro determinar o gráfico e a partir dele definir o domínio e a imagem da função. Vamos construir a reta que define a função para todos os valores de . Ficamos com essa reta:
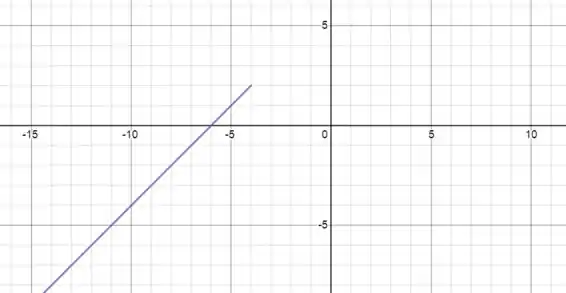
Agora vamos definir o gráfico para o 2º intervalo da função: para . Isso é o gráfico de uma semicircunferência de raio igual a . Assim:
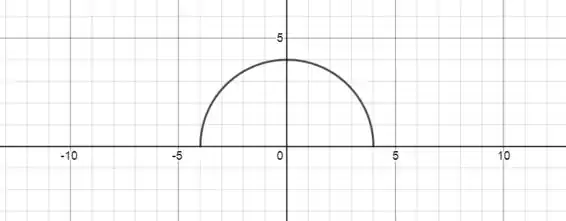
E a 3ª equação define a reta: . No gráfico ela fica:
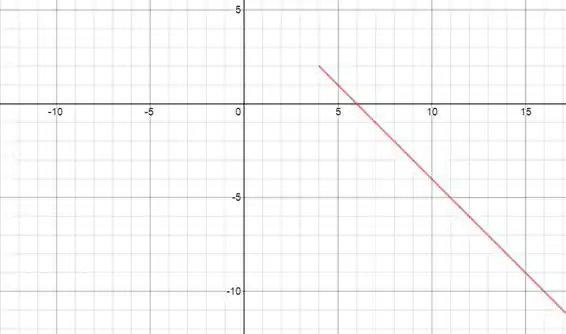
Agora vamos combinar os gráficos de cada uma dessas 3 funções e temos o gráfico da nossa função resultante:
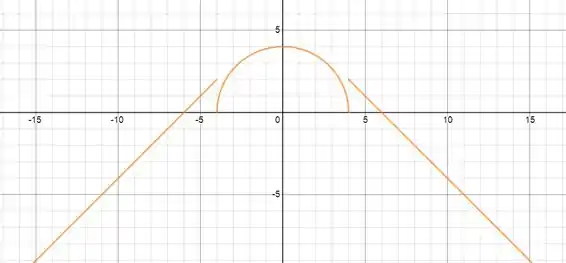
Esse é o gráfico da função!
Passo 2
Agora ficou fácil, né? Vemos que a função está definida para todos os valores de e que a imagem dela é
Repare que temos um intervalo aberto no 4, pois os pontos do raio não pertencem à semicircunferência, ou seja, o ponto não pertence à nossa função.
Resposta
Domínio:
Imagem:
