Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 64
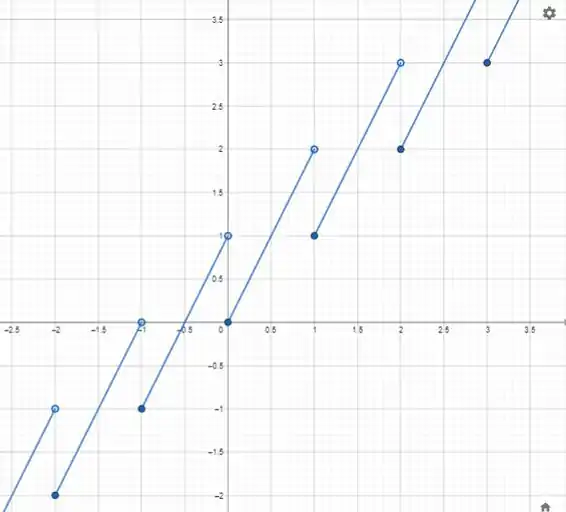
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico:
Passo 1
Vamos começar entendendo que diamos é aquela função , isso serve para o maior inteiro, menor ou igual a .
Essa é a função maior inteiro, você precisa determinar qual o intervalo de inteiror o número está. Por exemplo:
De forma geral, temos
Vai ter um valor constante em cada intervalo de inteiros.
Vamos entender o domínio da função agora. Tanto quando existem para qualquer valor de .
Então
Passo 2
Para entendermos a imagem, precisamos ver como sera a função em cada intervalo de inteiros, isso porque a funciona desse jeito.
Vamos pegar um intervalo qualquer de inteiros:
Assim a nossa fica:
Que é uma reta. Essa reta começa em inclusive, e termina em , sem incluir esse número.
Entao ela começa em e termina em .
O intervalo seguinte começa em , que é o próximo inteiro e termina em .
Repare que qualquer valor nos reais vai estar entre dois interios com essa diferença. Então a imagem são os próprios reais.
Passo 3
Vamos fazer o esboço
Para isso fazer as retas que vimos no último passo, em cada intervalo de inteiros.
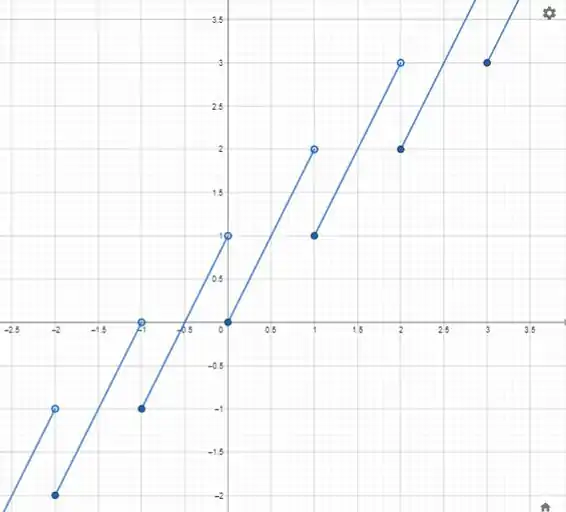
Resposta
