Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 29
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Para fazer o gráfico dessa função da forma que ela está, estaríamos assinando um atestado de loucura hehe. Então vamos tentar simplificar esses polinômios encontrando as raízes deles. Depois que simplificarmos a função, podemos esboçar o gráfico mais facilmente e depois do gráfico definir o domínio e a imagem é moleza.
Passo 2
Vamos começar fatorando a função quadrática do numerador.
Lembre-se que:
Onde e são as raízes do polinômio. Temos:
Vamos descobrir as raízes por bhaskara:
Daí temos nossas raízes:
E
Ou seja:
Podemos substituir isso na função original!
Passo 3
Agora fatorando o termo do numerador:
Vamos usar o mesmo princípio que usamos para fatorar o polinômio do numerador. Então precisamos das raízes. Por bhaskara:
Nossas duas raízes serão:
E
Então podemos reescrever o polinômio como:
Substituindo na função:
Agora podemos sair cortando tudo!
Passo 4
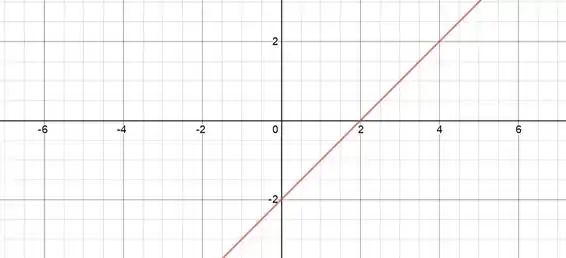
A era só polinômio do 1º grau no fim das contas! O gráfico dessa função então vai ser uma reta com inclinação que corta o eixo em . Fazendo o esboço:
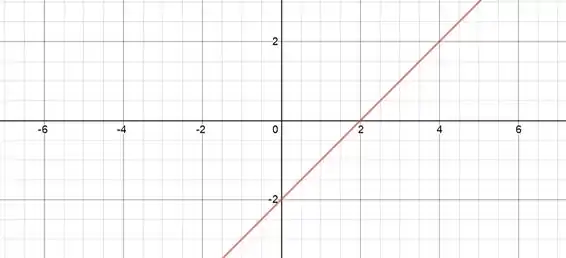
Passo 5
Do gráfico dá pra ver que temos uma reta que vai de até tanto no quanto no . Então o nosso domínio vai ser e a imagem também!
Resposta
Domínio:
Imagem:
