Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 27

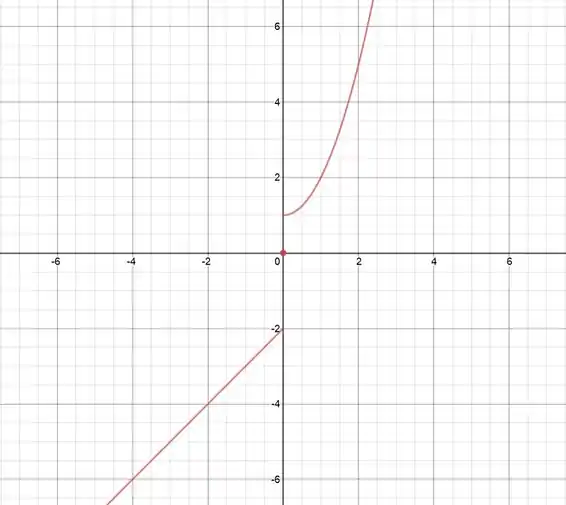
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.

Passo 1

Como temos uma função com 3 casos, um para cada intervalo, vamos começar plotando o gráfico para cada intervalo e depois analisamos o domínio e a imagem da função olhando pro gráfico que plotamos. Vamos devagarinho, intervalo por intervalo.

Passo 2

Para vamos ter a reta de equação . Essa é uma reta que cruza o eixo em e tem inclinação . É como se tivéssemos uma função , porém deslocada para baixo em unidades. Ficamos com:

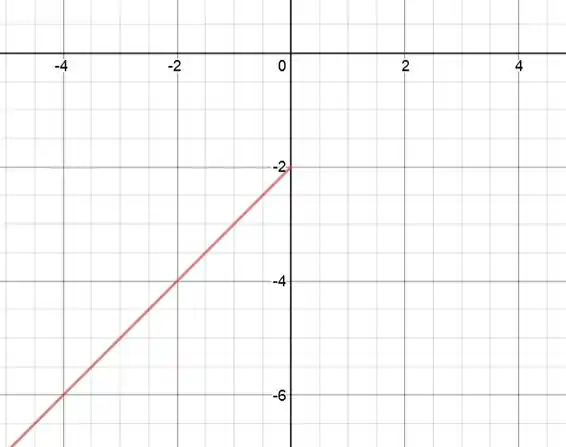
E assim como a função pede, estamos considerando apenas os valores para

Passo 3

Agora vamos incluir o que a 2ª linha pede:

Então teremos o ponto no nosso gráfico. Assim ó:

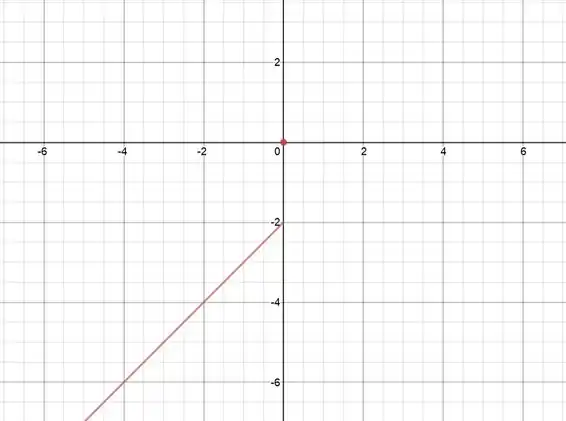
Agora é só acrescentar a última parte para e teremos o gráfico da função!

Passo 4

A 3ª parte da função da questão diz:

Um polinômio do 2º grau tem o gráfico de uma parábola! Mas como temos esse vamos ter que deslocar nossa parábola em unidade pra cima do . Vamos ficar com:

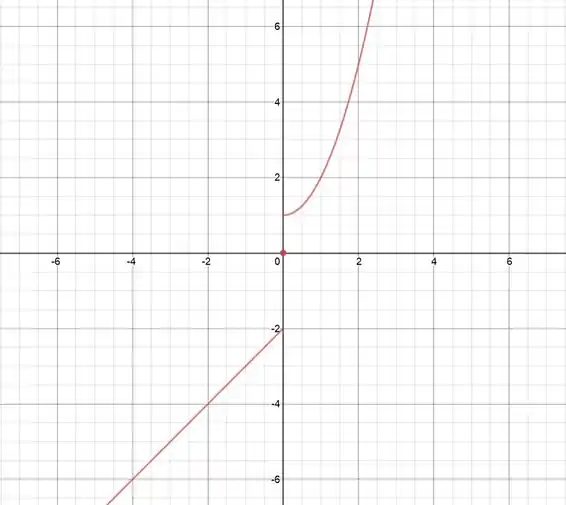
Esse é o gráfico da nossa função!

Passo 5

Agora olhando pro gráfico podemos definir o domínio e a imagem numa boa. A função está definida para todo valor de , então o domínio da função fica

E agora olhando pros valores que a função assume no eixo da pra ver que a reta garante todos os valores de até na nossa função. Repare que o não entra nesse intervalo! O ponto na origem garante o valor de e a parábola inclui todos os valores maiores que na imagem. Agora precisamos unir isso tudo para chegar no intervalo da função!