Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 24
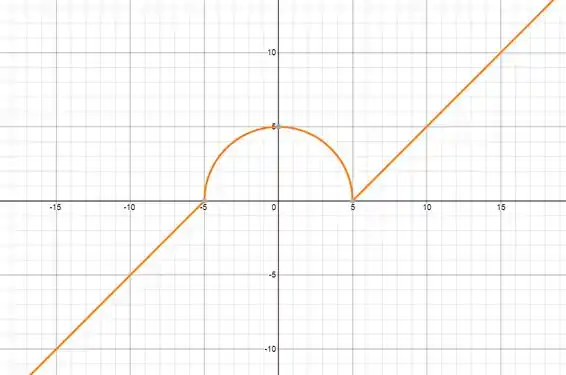
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Vamos começar verificando os valores que pode assumir, ou seja, o domínio da nossa função. De acordo com os intervalos, a nossa função está definida para todos os reais, porém temos que verificar aquela raiz quadrada e garantir que:
Ou seja:
Ou seja:
Isso até poderia restringir o nosso domínio, porém esses valores de são os valores para os quais a raiz está definida, então não muda nada. A nossa função está definidíssima para todos os reais: .
Passo 2
Perceba que as duas retas já garantem que nossa função esteja definida todos os reais exceto o valor . Mas podemos verificar que esse valor está dentro do intervalo intermediário da função. Vamos tentar satisfazer
Temos:
Tirando a raiz:
Vemos que e satisfazem essa equação, ou seja, também faz parte da imagem da nossa função. E com isso definimos a imagem da nossa equação para todos os reais.
Passo 3
E pra fechar a questão precisamos plotar o gráfico da função. Aquela parte intermediária define a equação de uma semicircunferência de raio :
Então temos uma semicircunferência de raio para os valores de em Fora disso teremos duas retas de mesma angulação continuando do fim de cada lado da circunferência, esse jeito:
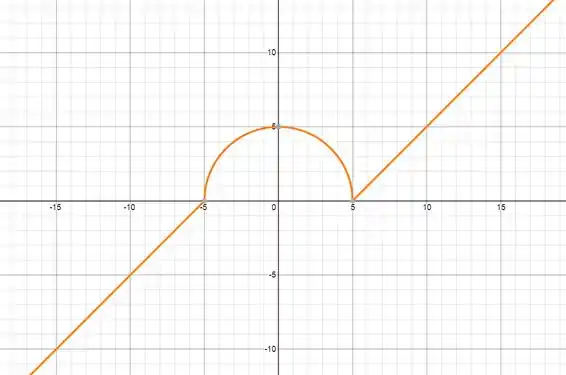
Resposta
Domínio:
Imagem:
