Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 37
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. Desenhe a superfície e o plano tangente.
Passo 1
E aiii minha turma, beleza!?
Nessa questão temos que determinar a equação do plano tangente a superfície parametrizada a seguir, e depois desenhar a superfície e o plano tangente nos pontos dados.
Vamos com calma, precisamos lembrar de algumas formulas aqui.
Esse estilo de parametrização é clássico, aquele que clamamos e .
Para obter um plano tangente para uma superfície parametrizada desse estilo, onde temos um vetor, devemos aplicar:
Onde, é ponto que queremos calcular. No nosso caso ele deu
Já, é o produto vetorial entre a derivada de em relação a e , também aplicado no ponto .
Feito isso, é substituir na equação acima, resolver o produto escalar e obter a expressão do plano tangente.
Para plotar os gráficos, devemos utilizar algum software conforme recomendação do livro. Você pode utilizar algum de sua preferência, porém aqui vamos utilizar o Geogebra 3D.
Vamos nessa então!!!
Passo 2
Vamos começar determinando a expressão do plano tangente.
Porém, antes vamos precisar calcular o produto vetorial .
Vamos começar derivando em relação a .
Derivando vamos ter:
Aplicando no ponto temos:
Agora, vamos derivar em relação a .
Derivando vamos ter:
Aplicando no ponto temos:
Passo 3
Agora que encontramos e :
Vamos aplicar o produto vetorial:
Vamos escrever na forma matricial:
Resolvendo esse determinante, vamos ter:
Agora, vamos substituir na equação do plano tangente os valores:
Sabemos que:
Substituindo, temos:
Resolvendo, ficamos com:
Que de forma reduzida ficará.
Portanto essa é a equação do plano tangente.
Passo 4
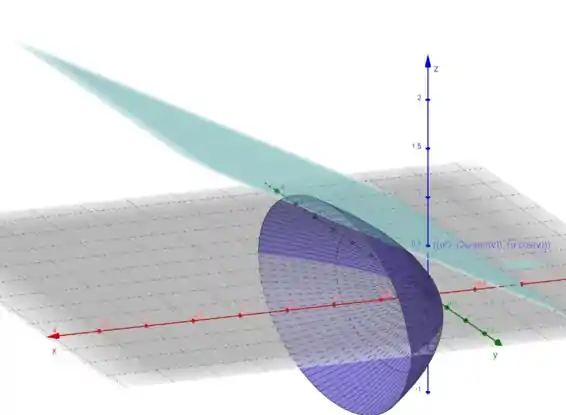
Agora vamos fazer um esboço da superfície parametrizada e do plano tangente.
Para isso, vamos utilizar o Geogebra 3D. Logo, temos:
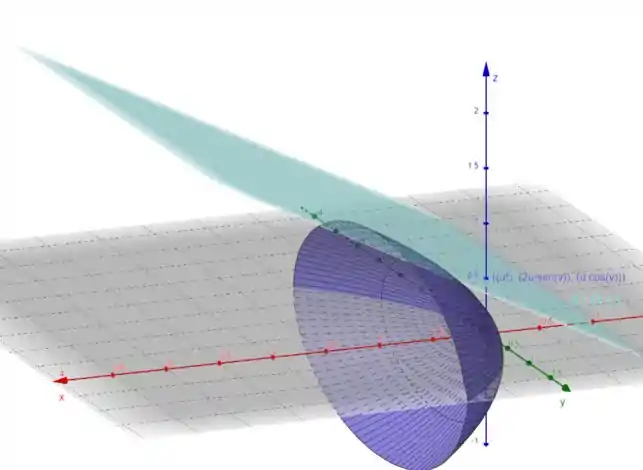
Resposta
